
【題目】如圖,某自來水公司要在公路兩側安裝排水管,公路為東西方向,在路北側沿直線![]() 排,在路南側沿直線
排,在路南側沿直線![]() 排,現要在矩形區域
排,現要在矩形區域![]() 內沿直線將
內沿直線將![]() 與
與![]() 接通.已知
接通.已知![]() ,
,![]() ,公路兩側排水管費用為每米1萬元,穿過公路的
,公路兩側排水管費用為每米1萬元,穿過公路的![]() 部分的排水管費用為每米2萬元,設
部分的排水管費用為每米2萬元,設![]() 與
與![]() 所成的小于
所成的小于![]() 的角為
的角為![]() .
.
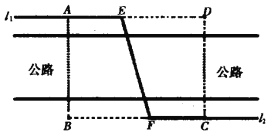
(Ⅰ)求矩形區域![]() 內的排水管費用
內的排水管費用![]() 關于
關于![]() 的函數關系;
的函數關系;
(Ⅱ)求排水管的最小費用及相應的角![]() .
.
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的運動方式,小王的微信朋友內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
性別 步數 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步數超過8000步被系統評定為“積極型”,否則為“懈怠型”,根據題意完成下面的2×2列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
積極型 | 懈怠型 | 總計 | |
男 | |||
女 | |||
總計 |
(2)若小王以這40位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選2人,其中每日走路不超過5000步的有X人,超過10000步的有Y人,設ξ=|X﹣Y|,求E的分布列及數學期望.
附:K2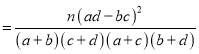 ,n=a+b+c+d.
,n=a+b+c+d.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 為
為![]() 的中點,
的中點,![]() .
.
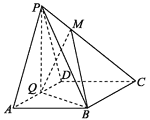
(1)求證:![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,
上,![]() ,試確定
,試確定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(3)若![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某氣象站統計了4月份甲、乙兩地的天氣溫度(單位![]() ),統計數據的莖葉圖如圖所示,
),統計數據的莖葉圖如圖所示,
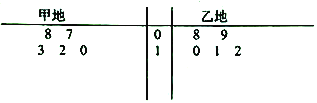
(1)根據所給莖葉圖利用平均值和方差的知識分析甲,乙兩地氣溫的穩定性;
(2)氣象主管部門要從甲、乙兩地各隨機抽取一天的天氣溫度,若甲、乙兩地的溫度之和大于或等于![]() ,則被稱為“甲、乙兩地往來溫度適宜天氣”,求“甲、乙兩地往來溫度適宜天氣”的概率.
,則被稱為“甲、乙兩地往來溫度適宜天氣”,求“甲、乙兩地往來溫度適宜天氣”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() =1(a>0,b>0)的一條漸近線方程為2x+y=0,且頂點到漸近線的距離為
=1(a>0,b>0)的一條漸近線方程為2x+y=0,且頂點到漸近線的距離為![]() .
.
(1)求此雙曲線的方程;
(2)設P為雙曲線上一點,A,B兩點在雙曲線的漸近線上,且分別位于第一、二象限,若![]() ,求△AOB的面積.
,求△AOB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018湖南(長郡中學、株洲市第二中學)、江西(九江一中)等十四校高三第一次聯考】已知函數![]() (其中
(其中![]() 且
且![]() 為常數,
為常數, ![]() 為自然對數的底數,
為自然對數的底數, ![]() ).
).
(Ⅰ)若函數![]() 的極值點只有一個,求實數
的極值點只有一個,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,若
時,若![]() (其中
(其中![]() )恒成立,求
)恒成立,求![]() 的最小值
的最小值![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知頂點是坐標原點的拋物線![]() 的焦點
的焦點![]() 在
在![]() 軸正半軸上,圓心在直線
軸正半軸上,圓心在直線![]() 上的圓
上的圓![]() 與
與![]() 軸相切,且
軸相切,且![]() 關于點
關于點![]() 對稱.
對稱.
(1)求![]() 和
和![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,與
,與![]() 交于
交于![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心為
的圓心為![]() ,直線l過點
,直線l過點![]() 且與x軸不重合,l交圓
且與x軸不重合,l交圓![]() 于C,D兩點,過
于C,D兩點,過![]() 作
作![]() 的平行線,交
的平行線,交![]() 于點E.設點E的軌跡為
于點E.設點E的軌跡為![]() .
.
(1)求![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 相切于點M,
相切于點M,![]() 與兩坐標軸的交點為A與B,直線
與兩坐標軸的交點為A與B,直線![]() 經過點M且與
經過點M且與![]() 垂直,
垂直,![]() 與
與![]() 的另一個交點為N,當
的另一個交點為N,當![]() 取得最小值時,求
取得最小值時,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com