【題目】已知橢圓
的上頂點為
，直線
與該橢圓交于
兩點，且點
恰為
的垂心，則直線的方程為______ .
【答案】
【解析】
設PQ直線y＝x+m，P（x1，y1），Q（x2，y2），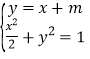
，3x2+4mx+2m2﹣2＝0，再由根的判別式和根與系數(shù)的關系進行求解．
上頂點
，右焦點F為垂心
因為
＝﹣1，且FM⊥l，
所以k1＝1，
所以設PQ直線y＝x+m，
且設P（x1，y1），Q（x2，y2）
由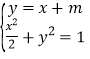
消y，得3x2+4mx+2m2﹣2＝0
△＝16m2﹣12（2m2﹣2）＞0，m2＜3
．
y1y2＝（x1+m）（x2+m）＝x1x2+m（x1+x2）+m2
．
又F為△MPQ的垂心，
∴PF⊥MQ，∴
又
∴
∴
，
∴
經(jīng)檢驗滿足m2＜3
∴存在滿足條件直線l方程為：x﹣y+1＝0，3x﹣3y﹣4＝0
∵x﹣y+1＝0過M點 即MP重合 不構(gòu)成三角形，
∴3x﹣3y﹣4＝0滿足題意．
故答案為：
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】某高校數(shù)學與統(tǒng)計學院為了對2018年錄取的大一新生有針對性地進行教學.從大一新生中隨機抽取40名，對他們在2018年高考的數(shù)學成績進行調(diào)查，統(tǒng)計發(fā)現(xiàn)40名新生的數(shù)學分數(shù)
分布在
內(nèi).當
時，其頻率
.
（Ⅰ）求
的值；
（Ⅱ）請在答題卡中畫出這40名新生高考數(shù)學分數(shù)的頻率分布直方圖，并估計這40名新生的高考數(shù)學分數(shù)的平均數(shù)；
（Ⅲ）從成績在100～120分的學生中，用分層抽樣的方法從中抽取5名學生，再從這5名學生中隨機選兩人甲、乙，記甲、乙的成績分別為
，求概率
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】定義域為
的函數(shù)
滿足：對于任意的實數(shù)
都有
成立，且當
時，
．
（Ⅰ）判斷函數(shù)的奇偶性，并證明你的結(jié)論；
（Ⅱ）證明在上為減函數(shù)；
（Ⅲ）若
，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點
、
的坐標分別是
，
，直線
，
相交于點
，且它們的斜率之積為
.
（1）求動點的軌跡方程；
（2）若過點
的直線
交動點的軌跡于
、
兩點， 且
為線段，的中點，求直線的方程.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
， 
.
（1）討論
的單調(diào)性；
（2）當
時，令
，其導函數(shù)為
，設
是函數(shù)
的兩個零點，判斷
是否為
的零點？并說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在三棱錐
， 
和
都是邊長為
的等邊三角形， 
， 
、
分別是
、
的中點.
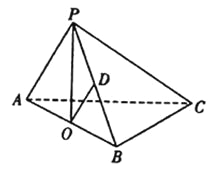
（1）求證： 
平面
；
（2）連接
，求證： 
平面
；
（3）求三棱錐
的體積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
