
【題目】已知函數(shù)![]()
(1)求f(x)的最小正周期及單調(diào)減區(qū)間;
(2)若α∈(0,π),且f![]() =
=![]() ,求tan
,求tan![]() 的值.
的值.
【答案】(1)最小正周期![]() ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為![]() (2)
(2)
【解析】分析:(1)根據(jù)原式結(jié)合二倍角公式,降冪公式,輔助角公式進(jìn)行化簡(jiǎn),然后計(jì)算周期,根據(jù)正弦函數(shù)的基本性質(zhì)求得單調(diào)區(qū)間;(2)∵f(![]() )=
)=![]() ,即sin
,即sin![]() =1. 可得α的值,然后按正切的和差公式打開(kāi)即可求解.
=1. 可得α的值,然后按正切的和差公式打開(kāi)即可求解.
解:(1)f(x)=(2cos2x-1)sin 2x+![]() cos 4x
cos 4x
=cos 2xsin 2x+![]() cos 4x
cos 4x
=![]() (sin 4x+cos 4x)
(sin 4x+cos 4x)
=![]() sin
sin![]() ,
,
∴f(x)的最小正周期T=![]() .
.
令2kπ+![]() ≤4x+
≤4x+![]() ≤2kπ+
≤2kπ+![]() π,k∈Z,
π,k∈Z,
得![]() +
+![]() ≤x≤
≤x≤![]() +
+![]() ,k∈Z.
,k∈Z.
∴f(x)的單調(diào)減區(qū)間為![]() ,k∈Z.
,k∈Z.
(2)∵f![]() =
=![]() ,
,
即sin![]() =1.
=1.
因?yàn)?/span>α/span>∈(0,π),-![]() <α-
<α-![]() <
<![]() ,
,
所以α-![]() =
=![]() ,故α=
,故α=![]() .
.
因此tan![]() =
=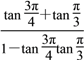 =
=![]() =2-
=2-![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
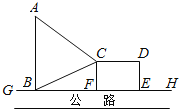
【題目】如圖,![]() 是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在
是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在![]() 上的一點(diǎn)
上的一點(diǎn)![]() 的正北方向的
的正北方向的![]() 處建一倉(cāng)庫(kù),并在公路同側(cè)建造一個(gè)正方形無(wú)頂中轉(zhuǎn)站
處建一倉(cāng)庫(kù),并在公路同側(cè)建造一個(gè)正方形無(wú)頂中轉(zhuǎn)站![]() (其中邊
(其中邊![]() 在
在![]() 上),現(xiàn)從倉(cāng)庫(kù)
上),現(xiàn)從倉(cāng)庫(kù)![]() 向
向![]() 和中轉(zhuǎn)站分別修兩條道路
和中轉(zhuǎn)站分別修兩條道路![]() ,
,![]() ,已知
,已知![]() ,且
,且![]() ,設(shè)
,設(shè)![]() ,
,![]() .
.
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)如果中轉(zhuǎn)站四周?chē)鷫Γ凑叫沃荛L(zhǎng))造價(jià)為![]() 萬(wàn)元
萬(wàn)元![]() ,兩條道路造價(jià)為
,兩條道路造價(jià)為![]() 萬(wàn)元
萬(wàn)元![]() ,問(wèn):
,問(wèn):![]() 取何值時(shí),該公司建中轉(zhuǎn)圍墻和兩條道路總造價(jià)
取何值時(shí),該公司建中轉(zhuǎn)圍墻和兩條道路總造價(jià)![]() 最低?
最低?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=|3x﹣4|.
(Ⅰ)記函數(shù)g(x)=f(x)+|x+2|﹣4,在下列坐標(biāo)系中作出函數(shù)g(x)的圖象,并根據(jù)圖象求出函數(shù)g(x)的最小值;
(Ⅱ)記不等式f(x)<5的解集為M,若p,q∈M,且|p+q+pq|<λ,求實(shí)數(shù)λ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線C: ![]() ,點(diǎn)
,點(diǎn) ![]() 在x軸的正半軸上,過(guò)點(diǎn)M的直線
在x軸的正半軸上,過(guò)點(diǎn)M的直線 ![]() 與拋物線C相交于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn).
與拋物線C相交于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn).
(1)若 ![]() ,且直線
,且直線 ![]() 的斜率為1,求以AB為直徑的圓的方程;
的斜率為1,求以AB為直徑的圓的方程;
(2)是否存在定點(diǎn)M,使得不論直線 ![]() 繞點(diǎn)M如何轉(zhuǎn)動(dòng),
繞點(diǎn)M如何轉(zhuǎn)動(dòng), ![]() 恒為定值?
恒為定值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓 ![]() 的離心率為
的離心率為 ![]() ,且過(guò)點(diǎn)
,且過(guò)點(diǎn) ![]() .
.
(1)求橢圓 ![]() 的方程;
的方程;
(2)設(shè)不過(guò)原點(diǎn) ![]() 的直線
的直線 ![]() 與橢圓
與橢圓 ![]() 交于
交于 ![]() 兩點(diǎn),直線
兩點(diǎn),直線 ![]() 的斜率分別為
的斜率分別為 ![]() ,滿(mǎn)足
,滿(mǎn)足 ![]() ,試問(wèn):當(dāng)
,試問(wèn):當(dāng) ![]() 變化時(shí),
變化時(shí), ![]() 是否為定值?若是,求出此定值,并證明你的結(jié)論;若不是,請(qǐng)說(shuō)明理由.
是否為定值?若是,求出此定值,并證明你的結(jié)論;若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
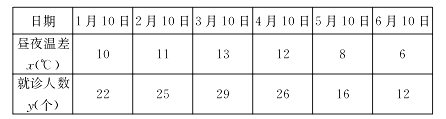
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數(shù)多少之間的關(guān)系,他們分別到氣象局與某醫(yī)院抄錄了1至6月每月10號(hào)的晝夜溫差情況與因患感冒而就診的人數(shù),得到如下的資料:
該興趣小組確定的研究方案是:現(xiàn)從這六組數(shù)據(jù)中選取2組,用剩下的4組數(shù)據(jù)求線性回歸方程,再用被選用的2組數(shù)據(jù)進(jìn)行檢驗(yàn).
參考公式: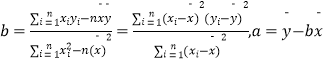
(1)求選取的2組數(shù)據(jù)恰好是相鄰兩個(gè)月的概率;
(2)若選取的是1月與6月的兩組數(shù)據(jù),請(qǐng)根據(jù)2至5月的數(shù)據(jù),求出 ![]() 關(guān)于
關(guān)于 ![]() 的線性回歸方程
的線性回歸方程 ![]() ;
;
(3)若有線性回歸方程得到的估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過(guò)2人,則認(rèn)為得到的線性回歸方程是理想的,試問(wèn)(2)中所得線性回歸方程是否是理想?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 方程
方程![]() 有兩個(gè)不等的負(fù)根,
有兩個(gè)不等的負(fù)根,![]() 方程
方程![]() 無(wú)實(shí)根,若“
無(wú)實(shí)根,若“![]() ”為真,“
”為真,“![]() ”為假,求實(shí)數(shù)
”為假,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com