
1、證明兩角差的余弦公式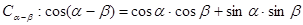 ;
;
2、由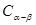 推導(dǎo)兩角和的余弦公式
推導(dǎo)兩角和的余弦公式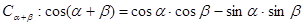 .
.
3、已知△ABC的面積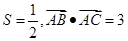 ,且
,且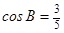 ,求
,求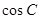 .
.
(1)在平面直角坐標(biāo)系中,以原點(diǎn)為圓心,作一單位圓,再以原點(diǎn)為頂點(diǎn),x軸非負(fù)半軸為始邊分別作角α,β.
設(shè)它們的終邊分別交單位圓于點(diǎn)P1(cosα,sinα),P2(cosβ,sinβ),即有兩單位向量,它們的所成角是|α-β|,根據(jù)向量數(shù)量積的性質(zhì)能夠證明cos(α-β)=cosαcosβ+sinαsinβ.
(2)先由誘導(dǎo)公式得sin(α+β)=cos(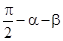 ),再進(jìn)一步整理為cos[(
),再進(jìn)一步整理為cos[(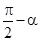 )-β],然后利用和差公式和誘導(dǎo)公式能夠得到sin(α+β)=sinαcosβ+cosαsinβ
)-β],然后利用和差公式和誘導(dǎo)公式能夠得到sin(α+β)=sinαcosβ+cosαsinβ
2、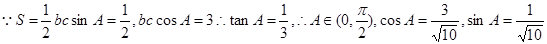
由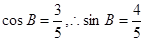 ,
,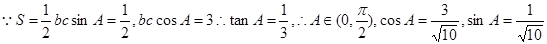
由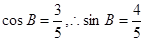 ,所以
,所以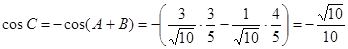
解析


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
在△ABC中,角A,B,C所對的邊分別為a,b,c,且滿足csinA=acosC.
(1)求角C的大小;
(2)求 sinA-cos
sinA-cos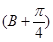 的最大值,并求取得最大值時角A,B的大小.
的最大值,并求取得最大值時角A,B的大小.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com