Question

（2009浙江卷理）（本題滿分15分）如圖，平面平面，

是以為斜邊的等腰直角三角形，分別為，

，的中點，，．

   （I）設(shè)是的中點，證明：平面；

   （II）證明：在內(nèi)存在一點，使平面，并求點到，的距離．

Answer 1

證明：（I）如圖，連結(jié)OP，以O(shè)為坐標(biāo)原點，分別以O(shè)B、OC、OP所在直線為軸，軸，軸，建立空間直角坐標(biāo)系O，.   

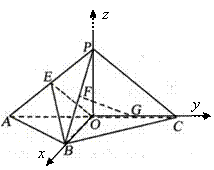則，由題意得，因，因此平面BOE的法向量為，得，又直線不在平面內(nèi)，因此有平面

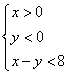（II）設(shè)點M的坐標(biāo)為，則，因為平面BOE，所以有，因此有，即點M的坐標(biāo)為，在平面直角坐標(biāo)系中，的內(nèi)部區(qū)域滿足不等式組，經(jīng)檢驗，點M的坐標(biāo)滿足上述不等式組，所以在內(nèi)存在一點，使平面，由點M的坐標(biāo)得點到，的距離為．.