
 中,
中, ,則A等于( )
,則A等于( ) 
 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
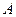 、
、 兩點的距離為
兩點的距離為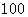 海里,
海里,
 在
在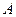 的北偏東
的北偏東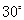 處,甲船自
處,甲船自 以
以 海里/小時的速度向
海里/小時的速度向 航行,同時乙船自
航行,同時乙船自 以
以 海里/小時的速度沿方位角
海里/小時的速度沿方位角 方向航行。問航行幾小時兩船之
方向航行。問航行幾小時兩船之 間的距離最短?
間的距離最短?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
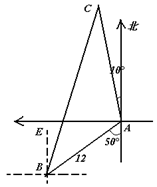
 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
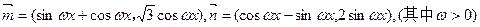 ,
, ,若
,若 相鄰兩對稱軸間的距離為
相鄰兩對稱軸間的距離為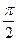 。
。 的值
的值 ,并求
,并求 的最大值及相應(yīng)x的集合;
的最大值及相應(yīng)x的集合; C的面積
C的面積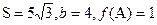 ,求邊a的長。
,求邊a的長。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 在△ABC中,
在△ABC中, 是它的三條邊,若
是它的三條邊,若 ,則△ABC是直角三角形,然而,若
,則△ABC是直角三角形,然而,若 ,則△ABC是銳角三角形,若
,則△ABC是銳角三角形,若 ,則△ABC是( )
,則△ABC是( )| A.銳角三角形 | B.直角三角形 | C.鈍角三角形 | D.由 的值確定 的值確定 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com