
已知函數(shù)![]()
(Ⅰ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)記f(x)在區(qū)間![]() (n∈N*)上的最小值為
(n∈N*)上的最小值為![]() ,
, ![]()
()如果對一切n,不等式![]() 恒成立,求實(shí)數(shù)c的取值范圍;
恒成立,求實(shí)數(shù)c的取值范圍;
()求證:![]() 。
。
解法一:
(I)因?yàn)?i>f(x)=ln(1+x)-x,所以函數(shù)定義域?yàn)椋?1,+![]() ),且
),且![]() =
=![]() -1=
-1=![]() .
.
由![]() >0得-1<x<0,f(x)的單調(diào)遞增區(qū)間為(-1,0);
>0得-1<x<0,f(x)的單調(diào)遞增區(qū)間為(-1,0);
由![]() <0得x>0,f(x)的單調(diào)遞增區(qū)間為(0,+
<0得x>0,f(x)的單調(diào)遞增區(qū)間為(0,+![]() ).
).
(II)因?yàn)?i>f(x)在[0,n]上是減函數(shù),所以bn=f(n)=ln(1+n)-n,
則an=ln(1+n)-bn=ln(1+n)-ln(1+n)+n=n.
(i)![]()
![]()
> ![]()
又lim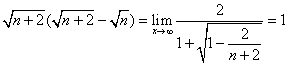 ,
,
因此![]() ,即實(shí)數(shù)c的取值范圍是(-
,即實(shí)數(shù)c的取值范圍是(-![]() ,
,![]() 。
。
(II)由(i)知![]()
因?yàn)閇![]() ]2
]2
![]()
所以![]()
![]() <
<![]() (n
(n![]() N*),
N*),
則![]() <
<
![]() 。
。
即![]() N*)
N*)![]()
解法二:
(Ⅰ)同解法一.
(Ⅱ)因?yàn)?i>f(x)在![]() 上是減函數(shù),所以
上是減函數(shù),所以![]()
則![]()
(i)因?yàn)?sub>![]() 對n∈N*恒成立.
對n∈N*恒成立.
所以![]() 對n∈N*恒成立.
對n∈N*恒成立.
則![]() 對n∈N*恒成立.
對n∈N*恒成立.
設(shè)![]() n∈N*,則c<g(n)對n∈N*恒成立.
n∈N*,則c<g(n)對n∈N*恒成立.
考慮![]()
因?yàn)?sub>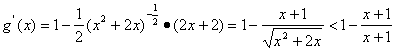 =0,
=0,
所以![]() 內(nèi)是減函數(shù);則當(dāng)n∈N*時(shí),g(n)隨n的增大而減小,
內(nèi)是減函數(shù);則當(dāng)n∈N*時(shí),g(n)隨n的增大而減小,
又因?yàn)?/p>
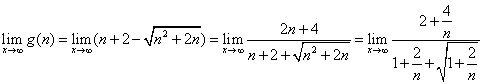 =1.
=1.
所以對一切![]() 因此c≤1,即實(shí)數(shù)c的取值范圍是(-∞,1].
因此c≤1,即實(shí)數(shù)c的取值范圍是(-∞,1].
() 由()知![]()
下面用數(shù)學(xué)歸納法證明不等式![]()
![]() (n
(n![]() N*),
N*),
①當(dāng)n=1時(shí),左邊=![]() ,右邊=
,右邊=![]() ,左邊<右邊.不等式成立.
,左邊<右邊.不等式成立.
②假設(shè)當(dāng)n=k時(shí),不等式成立.即![]()
![]()
當(dāng)n=k+1時(shí),
![]()
=![]()
即n=k+1時(shí),不等式成立
綜合①、②得,不等式![]() 成立.
成立.
所以![]()
![]()
![]()
即![]() 。
。


 全能測控一本好卷系列答案
全能測控一本好卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(08年龍巖一中沖刺理)(12分)
已知函數(shù)![]()
(1)求![]() 的最小正周期和單調(diào)增區(qū)間;
的最小正周期和單調(diào)增區(qū)間;
(2)求當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年河南省鄭州四中高考數(shù)學(xué)一輪復(fù)習(xí)綜合測試(一)(解析版) 題型:解答題
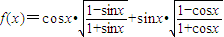
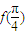 的值;
的值;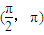 上的單調(diào)區(qū)間和值域.
上的單調(diào)區(qū)間和值域.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年北京市石景山區(qū)高三上學(xué)期期末考試數(shù)學(xué)理科試卷 題型:解答題
已知函數(shù)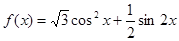 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在區(qū)間
在區(qū)間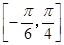 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年普通高中招生考試北京市高考理科數(shù)學(xué) 題型:解答題
(本小題共13分)
已知函數(shù)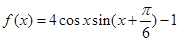 。
。
(Ⅰ)求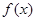 的最小正周期:
的最小正周期:
(Ⅱ)求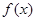 在區(qū)間
在區(qū)間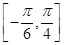 上的最大值和最小值。
上的最大值和最小值。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com