
��D����ֱ������A1B1C1��ABC�У�AB��AC��AB��AC��2��A1A��4���c(di��n)D��BC�����c(di��n)��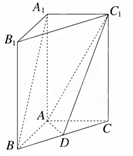
(1)����ֱ��A1B�cC1D���ɽǵ�����ֵ��
(2)��ƽ��ADC1�cƽ��ABA1�A�ǵ�����ֵ��
(1) ��(2)
��(2)
����ԇ�}��������?y��n)�ֱ��AB��AC�� �Ƀɴ�ֱ������A������(bi��o)ԭ�c(di��n)��������D��ʾ�Ŀ��gֱ������(bi��o)ϵ��
�Ƀɴ�ֱ������A������(bi��o)ԭ�c(di��n)��������D��ʾ�Ŀ��gֱ������(bi��o)ϵ��
��1������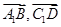 �քe��ֱ��A1B�cC1D�ķ������������
�քe��ֱ��A1B�cC1D�ķ������������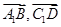 ������(bi��o)���ɿ��g�������A�ǹ�ʽ
������(bi��o)���ɿ��g�������A�ǹ�ʽ �ɵ�����
�ɵ�����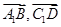 �A�ǵ�����ֵ��
�A�ǵ�����ֵ��
��2���O(sh��)ƽ�� �ķ�������
�ķ�������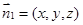 ��
��
�� ������(j��)���������x���ƽ��
������(j��)���������x���ƽ�� ��һ��(g��)������
��һ��(g��)������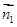 ����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/78/8/1zh7f2.png" style="vertical-align:middle;" />ƽ��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/78/8/1zh7f2.png" style="vertical-align:middle;" />ƽ��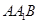 ��ȡƽ��
��ȡƽ��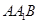 ��һ��(g��)��������
��һ��(g��)�������� �������
�������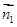 �c
�c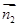 �A�ǵ�����ֵ����ƽ��ADC1�cƽ��ABA1�A���c
�A�ǵ�����ֵ����ƽ��ADC1�cƽ��ABA1�A���c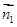 �c
�c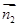 �A����Ȼ��a(b��)��
�A����Ȼ��a(b��)��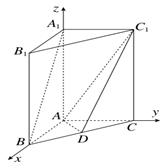
ԇ�}������(1)��A������(bi��o)ԭ�c(di��n)��������D��ʾ�Ŀ��gֱ������(bi��o)ϵ ���t
���t ��
�� ��
�� ��
�� ��
�� ��
�� ��
��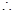 ����ֱ��
����ֱ�� �c
�c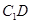 ���ɽǵ�����ֵ��
���ɽǵ�����ֵ�� ��
��
��2���O(sh��)ƽ�� �ķ�������
�ķ�������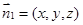 ��
�� ��
�� ����
����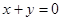 ��
��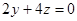 ��
��
��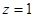 ���t
���t ��
�� ��ƽ��
��ƽ�� ��һ��(g��)��������
��һ��(g��)��������
ȡƽ��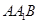 ��һ��(g��)��������
��һ��(g��)�������� ��
��
�O(sh��)ƽ�� �cƽ��
�cƽ��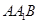 �A�ǵĴ�С��
�A�ǵĴ�С�� ����
���� ��
��
�� ����ƽ��
����ƽ�� �cƽ��
�cƽ��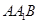 �A�ǵ�����ֵ��
�A�ǵ�����ֵ�� ��
��
���c(di��n)����1�����g����������(bi��o)�\(y��n)�㣻��2��ֱ������������ƽ�淨����������3�����ÿ��g��������ǡ�����ǣ�



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����ƽ��ֱ������(bi��o)ϵ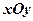 �У�����
�У�����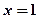 ��ʾ�^(gu��)�c(di��n)
��ʾ�^(gu��)�c(di��n)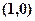 ��ƽ����
��ƽ����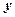 �S��ֱ��������ϽY(ji��)Փ�У��ڿ��gֱ������(bi��o)ϵ
�S��ֱ��������ϽY(ji��)Փ�У��ڿ��gֱ������(bi��o)ϵ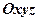 �У�����
�У�����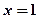 ��ʾ ��
��ʾ ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��ʾ��������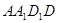 �c����
�c����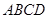 ����ƽ�滥�ഹֱ��
����ƽ�滥�ഹֱ��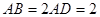 ���c(di��n)
���c(di��n)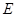 ��
��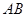 �����c(di��n).
�����c(di��n).
��1�����C�� ��ƽ��
��ƽ��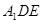 ����2�����C��
����2�����C��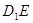
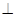
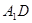 ��
��
��3���ھ���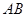 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)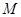 ��ʹ�����
��ʹ�����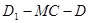 �Ĵ�С��
�Ĵ�С��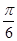 �������ڣ����
�������ڣ����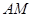 ���L(zh��ng)���������ڣ�Ո(q��ng)�f(shu��)������.
���L(zh��ng)���������ڣ�Ո(q��ng)�f(shu��)������.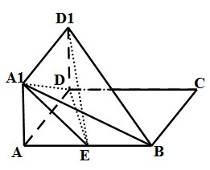
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D�������L(zh��ng)��a�������wABCD��A1B1C1D1�У�G���BC1D�����ģ�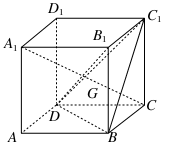
(1)���C��A1��G��C���c(di��n)������
(2)���C��A1C��ƽ��BC1D��
(3)���c(di��n)C��ƽ��BC1D�ľ��x��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����������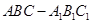 ��
�У�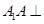 ƽ��
ƽ��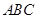 ��
��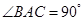 ��
��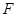 ����
����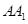 �ϵĄ�(d��ng)�c(di��n)��
�ϵĄ�(d��ng)�c(di��n)��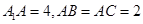 .
.
��(d��ng)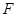 ��
��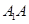 �����c(di��n)����ֱ��
�����c(di��n)����ֱ��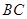 �cƽ��
�cƽ��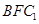 ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�Ʈ�(d��ng)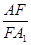 ��ֵ����ٕr(sh��)�������
��ֵ����ٕr(sh��)������� �Ĵ�С��45
�Ĵ�С��45 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����D��ʾ�Ķ����w�У�����BCFE�����Σ�EF//BC����EF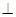 ƽ��AEB��AE
ƽ��AEB��AE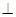 EB��AD//EF��BC=2AD=4��EF=3��AE=BE=2��G��BC�����c(di��n)��
EB��AD//EF��BC=2AD=4��EF=3��AE=BE=2��G��BC�����c(di��n)��
(1)���C��AB//ƽ��DEG��
(2)���C��BD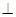 EG��
EG��
(3)������C��DF��E������ֵ��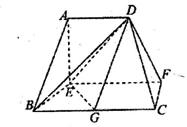
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��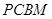 ��ֱ�����Σ���
��ֱ�����Σ���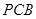 ��90�㣬
��90�㣬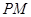 ��
��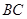 ��
��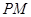 ��1��
��1��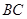 ��2����
��2����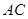 ��1����
��1����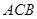 ��120�㣬
��120�㣬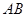 ��
��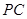 ��ֱ��
��ֱ��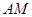 �cֱ��
�cֱ��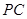 ���ɵĽǞ�60��.
���ɵĽǞ�60��.
��1��������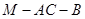 �ĵ�����ֵ��
�ĵ�����ֵ��
��2�����c(di��n) ����
����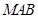 �ľ��x.
�ľ��x.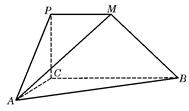
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ڿ��gֱ������(bi��o)ϵ�У���֪�c(di��n)A��1��0��2����B��1����3��1�����c(di��n)M��y�S�ϣ���M��A�c��B�ľ��x��ȣ��tM������(bi��o)�� ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com