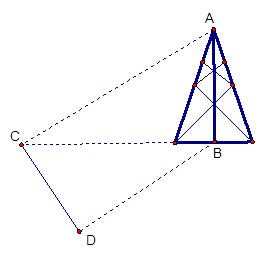
(10分) 測量河對岸的塔高

時,可以選與塔底

在同一水平面內(nèi)的兩個測點

與

.現(xiàn)測得

,并在點

測得塔頂
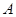
的仰角為

,求塔高

。
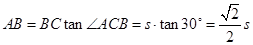
.
本題以實際問題為載體,主要考查了解三角形的實際應用.正弦定理、余弦定理是解三角形問題常用方法,應熟練記憶.先根據(jù)三角形內(nèi)角和為180°得∠CBD=180°-75°-60°=45°,再根據(jù)正弦定理求得BC,進而在Rt△ABC中,根據(jù)AB=BCtan∠ACB求得AB.
解:在

中,

由正弦定理得
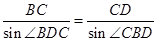
所以
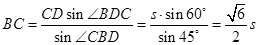
.
在
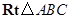
中,

.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)在
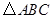
中,內(nèi)角
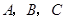
對邊的邊長分別是
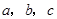
,已知
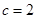
,

,
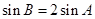
,求
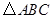
的面積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在△
ABC中,
a、
b、
c分別是角
A、
B、
C的對邊,且
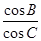
=-
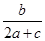
.
(1)求角
B的大小;
(2)若
b=
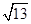
,
a+
c=4,求△
ABC的面積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知

、

、

為

的三內(nèi)角,且其對邊分別為

、

、

,若

.
(Ⅰ)求

; (Ⅱ)若

,求

的面積
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知向量

與

共線,設函數(shù)

。
(1)求函數(shù)

的周期及最大值;
(2)已知銳角 △ABC 中的三個內(nèi)角分別為 A、B、C,若有

,邊 BC=

,

,求 △ABC 的面積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在△ABC中,已知a=
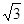
,
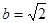
,B=45
0求A、C及c.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,為了測量河對岸A、B兩點之間的距離,觀察者找到一個點C,從C點可以觀察到點A、B;找到一個點D,從D點可以觀察到點A、C:找到一個點E,從E點可以觀察到點B、C。并測得以下數(shù)據(jù):CD=CE=100m,∠ACD=90°,∠ACB=45°,∠BCE=75°,∠CDA=∠CEB=60°,求A、B兩 點之間的距離。
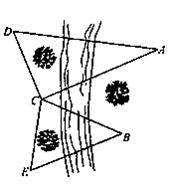
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在△ABC中,內(nèi)角A、B、C的對邊分別是a、b、c,若
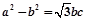
,
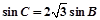
,則角A=
.
查看答案和解析>>

 時,可以選與塔底
時,可以選與塔底 在同一水平面內(nèi)的兩個測點
在同一水平面內(nèi)的兩個測點 與
與 .現(xiàn)測得
.現(xiàn)測得 ,并在點
,并在點 測得塔頂
測得塔頂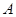 的仰角為
的仰角為 ,求塔高
,求塔高 。
。
 與
與  共線,設函數(shù)
共線,設函數(shù)  。
。 的周期及最大值;
的周期及最大值; ,邊 BC=
,邊 BC= ,
, ,求 △ABC 的面積.
,求 △ABC 的面積.