
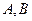 分別為橢圓
分別為橢圓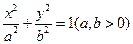 的左、右頂點,橢圓長半軸的長等于焦距,且
的左、右頂點,橢圓長半軸的長等于焦距,且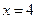 為它的右準線.
為它的右準線.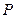 為右準線上不同于點(4,0)的任意一點,若直線
為右準線上不同于點(4,0)的任意一點,若直線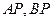 分別與橢圓相交于異于
分別與橢圓相交于異于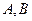 的點
的點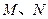 ,證明點
,證明點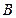 在以
在以 為直徑的圓內.
為直徑的圓內.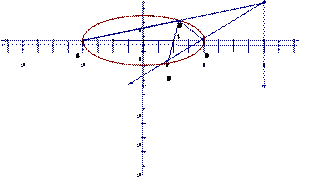
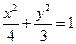
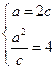 解得
解得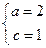 從而b=
從而b=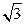 ,………………………………………3分
,………………………………………3分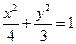 .……………………………………………………………………4分
.……………………………………………………………………4分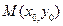 .
.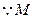 點在橢圓上,
點在橢圓上,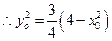 .……………………………………………………… 5分
.……………………………………………………… 5分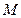 點異于頂點
點異于頂點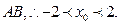
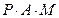 三點共線可得
三點共線可得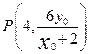 ,…………………………………………………………………6分
,…………………………………………………………………6分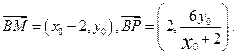 .……………………………………………………………7分
.……………………………………………………………7分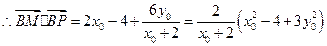 ,………………………………………………10分
,………………………………………………10分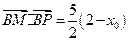 .…………………………………………………………12分
.…………………………………………………………12分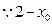 >0,
>0,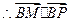 >0.于是
>0.于是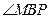 為銳角,從而
為銳角,從而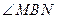 為鈍角,
為鈍角,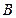 在以
在以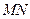 為直徑的圓內.………………………………………………………………………. 14分
為直徑的圓內.………………………………………………………………………. 14分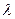 )(
)(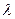
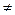 0),M(
0),M( ,
, ),N(
),N( ,
, ),則直線AP的方程為
),則直線AP的方程為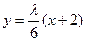 ,直線BP的方程為
,直線BP的方程為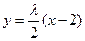 .…………………………….. 6分
.…………………………….. 6分 點M、N分別在直線AP、BP上,
點M、N分別在直線AP、BP上,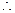
 =
=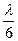 (
( +2),
+2), =
=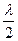 (
( -2).從而
-2).從而
 =
=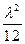 (
( +2)(
+2)( -2).③
-2).③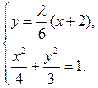 消去y得(27+
消去y得(27+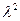 )
)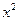 +4
+4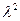 x+4(
x+4(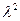 -27)=0………………8分
-27)=0………………8分
 ,-2是方程得兩根,
,-2是方程得兩根,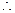 (-2).
(-2). ,即
,即 =
=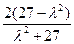 . ④
. ④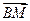 .
.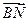 =(
=( -2,
-2,  ).(
).( -2,
-2, )=(
)=( -2)(
-2)( -2)+
-2)+
 . ⑤………9分
. ⑤………9分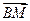 .
.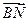 =
=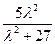 (
( -2)………………………………………………………… 12分
-2)………………………………………………………… 12分 N點在橢圓上,且異于頂點A、B,
N點在橢圓上,且異于頂點A、B,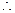
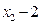 <0.
<0.
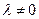 ,
,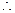
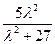 > 0, 從而
> 0, 從而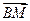 .
.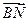 <0.
<0.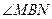
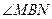 為鈍角,即點B在以MN為直徑的圓內………………………………14分
為鈍角,即點B在以MN為直徑的圓內………………………………14分 ,
, ),N(
),N( ,
, ),則-2<
),則-2< <2 , -2<
<2 , -2< <2.又MN的中點Q的坐標為(
<2.又MN的中點Q的坐標為(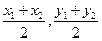 ),………………………………………5分
),………………………………………5分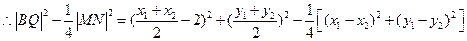
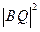 -
-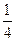
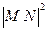 =(
=( -2)(
-2)( -2)+
-2)+
 . ⑥………………8分
. ⑥………………8分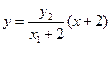 ,直線BP的方程為
,直線BP的方程為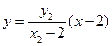 ………………10分
………………10分 點P在準線x=4上,
點P在準線x=4上,
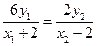 ,即
,即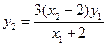 . ⑦
. ⑦ M點在橢圓上,
M點在橢圓上,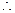
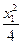 +
+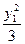 =1,即
=1,即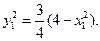 ⑧……… 12分
⑧……… 12分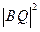 -
-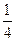
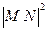 =
=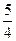
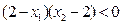 .
.

科目:高中數學 來源:不詳 題型:解答題
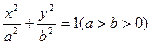 上一點,
上一點,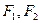 是橢圓的兩焦點,且滿足
是橢圓的兩焦點,且滿足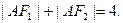
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 軸上,橢圓C上的點到焦點的最大值為3,最小值為1.
軸上,橢圓C上的點到焦點的最大值為3,最小值為1. :
: 與
與 橢圓交于不同的兩點M,N(M,N不是左、右頂點),且以MN為直徑的圓經過橢圓的右頂點A.求證:直線
橢圓交于不同的兩點M,N(M,N不是左、右頂點),且以MN為直徑的圓經過橢圓的右頂點A.求證:直線 過定點,并求出定點的坐標.
過定點,并求出定點的坐標.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
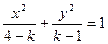 給出下面四個命題:
給出下面四個命題: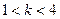 時,曲線C表示橢圓;
時,曲線C表示橢圓;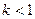 或
或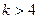
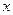 軸上的橢圓,則
軸上的橢圓,則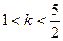
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
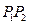 是冰川的部分邊界線(不考慮其他邊界),當冰川融化時,邊界線沿與其垂直的方向朝考察區域平行移動,第一年移動0.2km,以后每年移動的距離為前一年的2倍。問:經過多長時間,點A恰好在冰川邊界線上?
是冰川的部分邊界線(不考慮其他邊界),當冰川融化時,邊界線沿與其垂直的方向朝考察區域平行移動,第一年移動0.2km,以后每年移動的距離為前一年的2倍。問:經過多長時間,點A恰好在冰川邊界線上?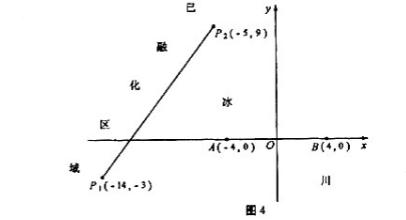
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com