
已知函數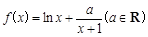 .
.
(Ⅰ)當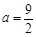 時,如果函數
時,如果函數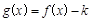 僅有一個零點,求實數
僅有一個零點,求實數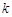 的取值范圍;
的取值范圍;
(Ⅱ)當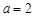 時,試比較
時,試比較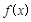 與1的大小;
與1的大小;
(Ⅲ)求證: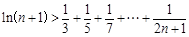
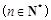 .
.
(Ⅰ)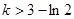 或
或
(Ⅱ)①當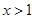 時,
時, ,即
,即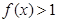 ;
;
②當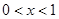 時,
時,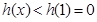 ,即
,即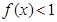 ;
;
③當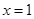 時,
時,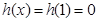 ,即
,即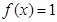 .
.
(Ⅲ)見解析
【解析】(I)當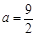 時,g(x)=f(x)-k有一個零點,實質是y=f(x)與直線y=k有一個公共點,所以利用導數研究y=f(x)的單調性,極值,最值,作出圖像可求出k的取值范圍.
時,g(x)=f(x)-k有一個零點,實質是y=f(x)與直線y=k有一個公共點,所以利用導數研究y=f(x)的單調性,極值,最值,作出圖像可求出k的取值范圍.
(II)當a=2時,令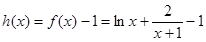 ,然后利用導數研究其單調區間及最值,然后再分類討論f(x)與1的大小關系.
,然后利用導數研究其單調區間及最值,然后再分類討論f(x)與1的大小關系.
(III)解本小題的關鍵是根據(2)的結論,當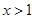 時,
時,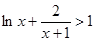 ,即
,即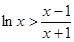 .
.
令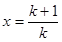 ,則有
,則有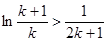 ,從而得
,從而得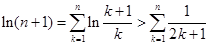 ,問題得解.
,問題得解.
解:(Ⅰ)當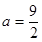 時,
時,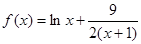 ,定義域是
,定義域是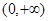 ,
,
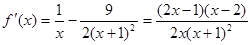 , 令
, 令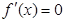 ,得
,得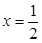 或
或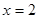 . …2分
. …2分
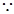 當
當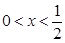 或
或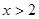 時,
時,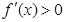 ,當
,當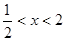 時,
時,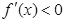 ,
,
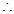 函數
函數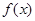 在
在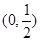 、
、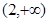 上單調遞增,在
上單調遞增,在 上單調遞減. ……………4分
上單調遞減. ……………4分
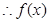 的極大值是
的極大值是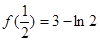 ,極小值是
,極小值是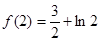 .
.
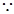 當
當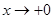 時,
時,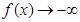 ;
;  當
當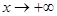 時,
時,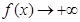 ,
,
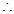 當
當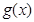 僅有一個零點時,
僅有一個零點時,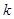 的取值范圍是
的取值范圍是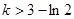 或
或 .……………5分
.……………5分
(Ⅱ)當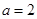 時,
時,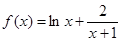 ,定義域為
,定義域為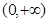 .
.
令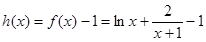 ,
,
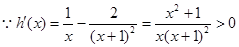 ,
, 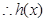 在
在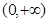 上是增函數. ………7分
上是增函數. ………7分
①當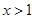 時,
時, ,即
,即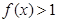 ;
;
②當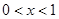 時,
時,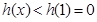 ,即
,即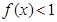 ;
;
③當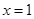 時,
時,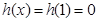 ,即
,即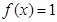 .……………9分
.……………9分
(Ⅲ)(法一)根據(2)的結論,當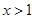 時,
時,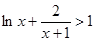 ,即
,即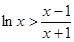 .
.
令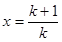 ,則有
,則有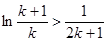 ,
,
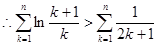 . ……………12分
. ……………12分
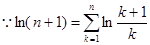 ,
,  . ……………14分
. ……………14分
(法二)當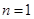 時,
時,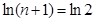 .
.
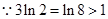 ,
,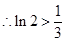 ,即
,即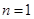 時命題成立.…………………10分
時命題成立.…………………10分
設當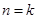 時,命題成立,即
時,命題成立,即 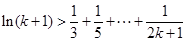 .
.
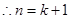 時,
時,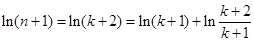
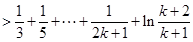 .
.
根據(Ⅱ)的結論,當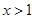 時,
時,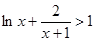 ,即
,即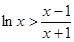 .
.
令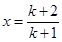 ,則有
,則有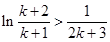 ,
,
則有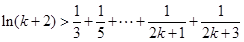 ,即
,即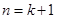 時命題也成立.……………13分
時命題也成立.……………13分
因此,由數學歸納法可知不等式成立.……………………14分
(法三)如圖,根據定積分的定義,
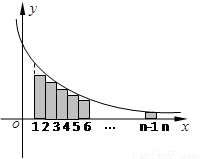
得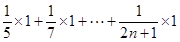
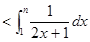 .……11分
.……11分
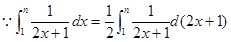
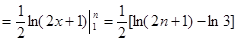 ,
,
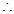
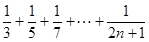
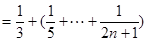

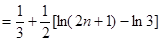 .……………………12分
.……………………12分
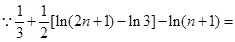
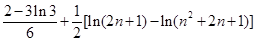 ,
,
又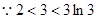 ,
,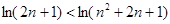 ,
,
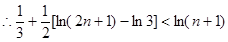 .
.
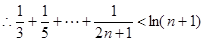 .………………14分
.………………14分


 科學實驗活動冊系列答案
科學實驗活動冊系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com