
【題目】如圖所示,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() ,
, ![]() 分別是
分別是![]() 的中點.
的中點.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的大小為
的大小為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ)連接![]() ,
, ![]() ,由中位線的性質可得:
,由中位線的性質可得: ![]() ,利用線面平行的判斷定理即可證得
,利用線面平行的判斷定理即可證得![]() 平面
平面![]() .
.
(Ⅱ)結合直三棱柱的性質,分別以![]() ,
, ![]() ,
, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立如圖所示的空間直角坐標系.設
軸建立如圖所示的空間直角坐標系.設![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,據此可得平面
,據此可得平面![]() 的一個法向量為
的一個法向量為![]() ,平面
,平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則![]() ,求解方程可得
,求解方程可得![]() ,利用線面角的向量求法可得
,利用線面角的向量求法可得![]() .
.
試題解析:
(Ⅰ)連接![]() ,
, ![]() ,則
,則![]() 且
且![]() 為
為![]() 的中點,
的中點,
又![]()
![]() 為
為![]() 的中點,
的中點, ![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(Ⅱ)因為![]() 是直三棱柱,所以
是直三棱柱,所以![]() 平面
平面![]() ,得
,得![]() .因為
.因為![]() ,
, ![]() ,
,
![]() ,故
,故![]() .以
.以![]() 為原點,分別以
為原點,分別以![]() ,
, ![]() ,
, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立如圖所示的空間直角坐標系.
軸建立如圖所示的空間直角坐標系.
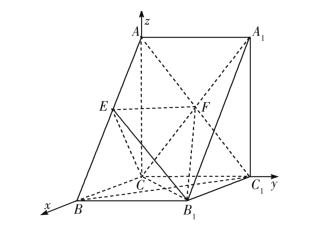
設![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
取平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由![]() 得
得![]() :令
:令![]() ,得
,得![]() ,
,
同理可得平面![]() 的一個法向量為
的一個法向量為![]() ,
,
![]() 二面角
二面角![]() 的大小為
的大小為![]() ,
, ![]() ,
,
解得![]() ,得
,得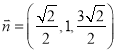 ,又
,又![]() ,
,
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則![]()
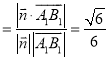 .
.


 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源: 題型:
【題目】一只藥用昆蟲的產卵數y與一定范圍內的溫度x有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
溫度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
產卵數y/個 | 6 | 11 | 20 | 27 | 57 | 77 |
經計算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,線性回歸模型的殘差平方和
,線性回歸模型的殘差平方和![]() ,e8.0605≈3167,其中xi, yi分別為觀測數據中的溫度和產卵數,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分別為觀測數據中的溫度和產卵數,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用線性回歸模型,求y關于x的回歸方程![]() =
=![]() x+
x+![]() (精確到0.1);
(精確到0.1);
(Ⅱ)若用非線性回歸模型求得y關于x的回歸方程為![]() =0.06e0.2303x,且相關指數R2=0.9522.
=0.06e0.2303x,且相關指數R2=0.9522.
( i )試與(Ⅰ)中的回歸模型相比,用R2說明哪種模型的擬合效果更好.
( ii )用擬合效果好的模型預測溫度為35C時該種藥用昆蟲的產卵數(結果取整數).
附:一組數據(x1,y1), (x2,y2), ...,(xn,yn ), 其回歸直線![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估計為
的斜率和截距的最小二乘估計為

![]() =
=![]()
![]() ;相關指數R2=
;相關指數R2= .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某城市街道上一側路邊邊緣![]() 某處安裝路燈,路寬
某處安裝路燈,路寬![]() 為
為![]() 米,燈桿
米,燈桿![]() 長4米,且與燈柱
長4米,且與燈柱![]() 成
成![]() 角,路燈采用可旋轉燈口方向的錐形燈罩,燈罩軸線
角,路燈采用可旋轉燈口方向的錐形燈罩,燈罩軸線![]() 與燈的邊緣光線(如圖
與燈的邊緣光線(如圖![]() ,
, ![]() )都成
)都成![]() 角,當燈罩軸線
角,當燈罩軸線![]() 與燈桿
與燈桿![]() 垂直時,燈罩軸線正好通過
垂直時,燈罩軸線正好通過![]() 的中點.
的中點.
(I)求燈柱![]() 的高
的高![]() 為多少米;
為多少米;
(II)設![]() ,且
,且![]() ,求燈所照射路面寬度
,求燈所照射路面寬度![]() 的最小值.
的最小值.

查看答案和解析>>
科目:高中數學 來源: 題型:
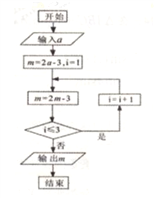
【題目】《算法統宗》是中國古代數學名著,由明代數學家程大位所著,該著作完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉變,對我國民間普及珠算和數學知識起到了很大的作用,如圖所示的程序框圖的算法思路源于該著作中的“李白沽酒”問題,執行該程序框圖,若輸出的![]() 的值為0,則輸入的
的值為0,則輸入的![]() 的值為( )
的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018貴州遵義市高三上學期第二次聯考】設拋物線![]() 的準線與
的準線與![]() 軸交于
軸交于![]() ,拋物線的焦點為
,拋物線的焦點為![]() ,以
,以![]() 為焦點,離心率
為焦點,離心率![]() 的橢圓與拋物線的一個交點為
的橢圓與拋物線的一個交點為 ;自
;自![]() 引直線交拋物線于
引直線交拋物線于![]() 兩個不同的點,設
兩個不同的點,設![]() .
.
(Ⅰ)求拋物線的方程和橢圓的方程;
(Ⅱ)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com