
(13分)已知數(shù)列![]() 滿足:
滿足:![]() 其中
其中![]() ,數(shù)列
,數(shù)列![]() 滿足:
滿足:![]()
(1)求![]() ;
;
(2)求數(shù)列![]() 的通項公式;
的通項公式;
(3)是否存在正數(shù)k,使得數(shù)列![]() 的每一項均為整數(shù),如果不存在,說明理由,如果存在,求出所有的k.
的每一項均為整數(shù),如果不存在,說明理由,如果存在,求出所有的k.
解析:(1)經(jīng)過計算可知:![]()
![]() .
.
求得![]() .…………………………………………(4分)
.…………………………………………(4分)
(2)由條件可知:![]() .…………①
.…………①
類似地有:![]() .…………②
.…………②
①-②有:![]() .
.
即:![]() .
.
![]() 因此:
因此:![]()
![]()
即:![]() 故
故![]()
![]()
所以:![]() .…………………………………………(8分)
.…………………………………………(8分)
(3)假設(shè)存在正數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 的每一項均為整數(shù).
的每一項均為整數(shù).
則由(2)可知: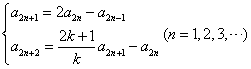 …………③
…………③
由![]() ,及
,及![]() 可知
可知![]() .
.
當(dāng)![]() 時,
時,![]() 為整數(shù),利用
為整數(shù),利用![]() ,結(jié)合③式,反復(fù)遞推,可知
,結(jié)合③式,反復(fù)遞推,可知![]() ,
,![]() ,
,![]() ,
,![]() ,…均為整數(shù).
,…均為整數(shù).
當(dāng)![]() 時,③變?yōu)?IMG height=69 src='http://thumb.zyjl.cn/pic1/img/20090521/20090521210518028.gif' width=220>………④
時,③變?yōu)?IMG height=69 src='http://thumb.zyjl.cn/pic1/img/20090521/20090521210518028.gif' width=220>………④
我們用數(shù)學(xué)歸納法證明![]() 為偶數(shù),
為偶數(shù),![]() 為整數(shù)
為整數(shù)![]()
![]() 時,結(jié)論顯然成立,假設(shè)
時,結(jié)論顯然成立,假設(shè)![]() 時結(jié)論成立,這時
時結(jié)論成立,這時![]() 為偶數(shù),
為偶數(shù),![]() 為整數(shù),故
為整數(shù),故![]() 為偶數(shù),
為偶數(shù),![]() 為整數(shù),所以
為整數(shù),所以![]() 時,命題成立.
時,命題成立.
故數(shù)列![]() 是整數(shù)列.
是整數(shù)列.
綜上所述,![]() 的取值集合是
的取值集合是![]() .………………………………………(13分)
.………………………………………(13分)


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2012屆廣東省廣州六中高三上學(xué)期第三次月考文科數(shù)學(xué)試卷(帶解析) 題型:解答題
(本小題滿分14分)
已知數(shù)列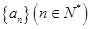 滿足:
滿足: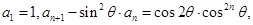 其中
其中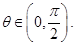
(1)當(dāng)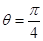 時,求
時,求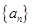 的通項公式;
的通項公式;
(2)在(1)的條件下,若數(shù)列 中,
中,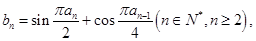 且
且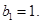 求證:對于
求證:對于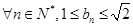 恒成立;
恒成立;
(3)對于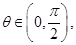 設(shè)
設(shè)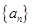 的前
的前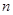 項和為
項和為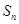 ,試比較
,試比較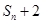 與
與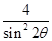 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年浙江省溫州中學(xué)高二下學(xué)期期末考試數(shù)學(xué)(文)試題 題型:解答題
已知數(shù)列 滿足
滿足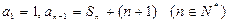 ,其中
,其中 為
為 的前
的前 項和,
項和,
(1)用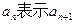 ;
;
(2)證明數(shù)列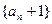 是等比數(shù)列;
是等比數(shù)列;
(3)求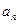 和
和 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年廣東省高三高考預(yù)測數(shù)學(xué)試卷(解析版) 題型:選擇題
已知數(shù)列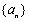 滿足
滿足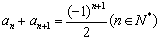 ,其中
,其中 ,試通過計算
,試通過計算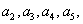 猜想
猜想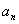 等于( )
等于( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣東省高三上學(xué)期第三次月考文科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分14分)
已知數(shù)列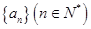 滿足:
滿足: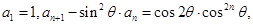 其中
其中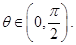
(1)當(dāng)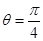 時,求
時,求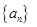 的通項公式;
的通項公式;
(2)在(1)的條件下,若數(shù)列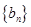 中,
中,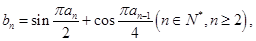 且
且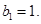 求證:對于
求證:對于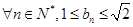 恒成立;
恒成立;
(3)對于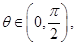 設(shè)
設(shè)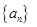 的前
的前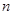 項和為
項和為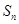 ,試比較
,試比較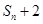 與
與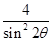 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年浙江省高二下學(xué)期期末考試數(shù)學(xué)(文)試題 題型:解答題
已知數(shù)列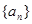 滿足
滿足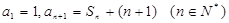 ,其中
,其中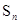 為
為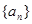 的前
的前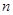 項和,
項和,
(1)用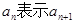 ;
;
(2)證明數(shù)列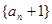 是等比數(shù)列;
是等比數(shù)列;
(3)求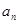 和
和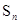 。
。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com