Question

【題目】如圖所示，等腰梯形ABCD的底角A等于60°．直角梯形ADEF所在的平面垂直于平面 ABCD，∠EDA=90°，且ED=AD=2AF=2AB=2．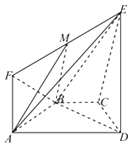

（Ⅰ）證明：平面ABE⊥平面EBD；
（Ⅱ）點M在線段EF上，試確定點M的位置，使平面MAB與平面ECD所成的角的余弦值為 ．

Answer 1

【答案】（I）證明：∵平面ABCD⊥平面ADEF，平面ABCD∩平面ADEF=AD，ED⊥AD，ED平面ADEF， ∴ED⊥平面ABCD，∵AB平面ABCD，
∴ED⊥AD，
∵AB=1，AD=2，∠BAD=60°，
∴BD= = ，
∴AB2+BD2=AD2 ， ∴AB⊥BD，
又BD平面BDE，ED平面BDE，BD∩ED=D，
∴AB⊥平面BDE，又AB平面ABE，
∴平面ABE⊥平面EBD．
（II）解：以B為原點，以BA，BD為x軸，y軸建立空間直角坐標系B﹣xyz，
則A（1，0，0），B（0，0，0），C（﹣ ， ，0），D（0， ，0），E（0， ，2），
F（1，0，1），則 =（ ， ，0）， =（0，0，2）， =（1，0，0）， =（1，﹣ ，﹣1），
設 =λ =（λ，﹣ λ，﹣λ）（0≤λ≤1），則 = + =（λ， ﹣ ，2﹣λ），
設平面CDE的法向量為 =（x1 ， y1 ， z1），平面ABM的法向量為 =（x2 ， y2 ， z2），
則 ， ，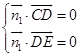
∴ ， ，
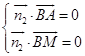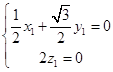令y1=1得 =（﹣ ，1，0），令y2=2﹣λ得 =（0，2﹣λ， ），
∴cos＜ ＞= = = ，解得λ= ，
∴當M為EF的中點時，平面MAB與平面ECD所成的角的余弦值為 ．

【解析】（I）計算BD，根據勾股定理逆定理得出AB⊥BD，再根據ED⊥平面ABCD得出ED⊥AB，故而AB⊥平面ADEF，從而平面ABE⊥平面EBD；（II）建立空間坐標系，設 =λ ，求出兩平面的法向量，令法向量的夾角余弦值的絕對值等于 ，解出λ即可得出結論．
【考點精析】認真審題，首先需要了解平面與平面垂直的判定(一個平面過另一個平面的垂線，則這兩個平面垂直)．