
動圓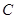 與定圓
與定圓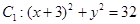 內切,與定圓
內切,與定圓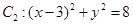 外切,A點坐標為
外切,A點坐標為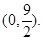 (1)求動圓
(1)求動圓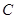 的圓心
的圓心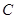 的軌跡方程和離心率;(2)若軌跡
的軌跡方程和離心率;(2)若軌跡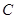 上的兩點
上的兩點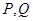 滿足
滿足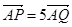 ,求
,求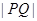 的值.
的值.
(1) ,離心率為
,離心率為 ;(2)
;(2) .
.
【解析】本試題主要是考查了運用定義法求解軌跡方程以及直線與圓錐曲線的位置關系的綜合運用。
(1)利用圓與圓的位置關系,結合圓心距和半徑的關系,得到動點的軌跡滿足橢圓的定義,然后結合定義得到軌跡方程。
(2)設出直線方程與橢圓方程聯立方程組,然后結合韋達定理和向量的關系式的,到坐標關系,進而化簡得到點的坐標。
(1)如圖,設動圓C的半徑為R,

則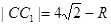 ,①
,①
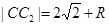 ,②
,②
①+②得,
由橢圓的定義知 點的軌跡是以
點的軌跡是以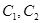 為焦點,長軸長為
為焦點,長軸長為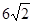 的橢圓,其軌跡方程為
的橢圓,其軌跡方程為 ,離心率為
,離心率為 ……………………………………………………………………6分
……………………………………………………………………6分
(2)設
由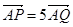 可得
可得
所以 ③…………………………………9分
③…………………………………9分
由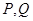 是橢圓
是橢圓 上的兩點,得
上的兩點,得
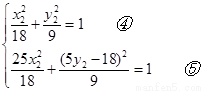 ,由④、⑤得
,由④、⑤得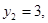
將 代入③,得
代入③,得 ,將
,將 代入④,得
代入④,得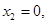 所以
所以 ,
,
所以 .…………………………………………13分
.…………………………………………13分


科目:高中數學 來源:2012-2013學年天津市天津一中高二上學期期中考試理科數學試卷(帶解析) 題型:解答題
動圓 與定圓
與定圓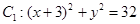 內切,與定圓
內切,與定圓 外切,A點坐標為
外切,A點坐標為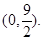 (1)求動圓
(1)求動圓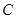 的圓心
的圓心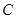 的軌跡方程和離心率;(2)若軌跡
的軌跡方程和離心率;(2)若軌跡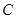 上的兩點
上的兩點 滿足
滿足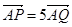 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2013屆湖北省武漢市高二下期末文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)
動圓G與圓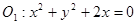 外切,同時與圓
外切,同時與圓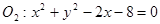 內切,設動圓圓心G的軌跡為
內切,設動圓圓心G的軌跡為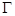 。
。
(1)求曲線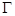 的方程;
的方程;
(2)直線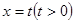 與曲線
與曲線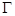 相交于不同的兩點
相交于不同的兩點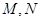 ,以
,以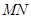 為直徑作圓
為直徑作圓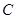 ,若圓C與
,若圓C與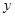 軸相交于兩點
軸相交于兩點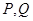 ,求
,求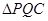 面積的最大值;
面積的最大值;
(3)設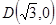 ,過
,過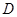 點的直線
點的直線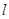 (不垂直
(不垂直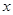 軸)與曲線
軸)與曲線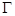 相交于
相交于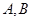 兩點,與
兩點,與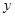 軸交于點
軸交于點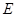 ,若
,若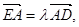
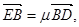 試探究
試探究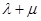 的值是否為定值,若是,求出該定值,若不是,請說明理由。
的值是否為定值,若是,求出該定值,若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源:2013屆江西省四校高二下學期第三次月考理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)
動圓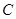 與定圓
與定圓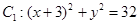 內切,與定圓
內切,與定圓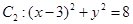 外切,A點坐標為
外切,A點坐標為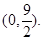
(1)求動圓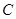 的圓心
的圓心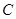 的軌跡方程和離心率;
的軌跡方程和離心率;
(2)若軌跡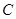 上的兩點
上的兩點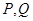 滿足
滿足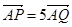 ,求
,求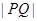 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com