
【題目】已知函數f(x)=bax , (其中a,b為常數且a>0,a≠1)的圖象經過點A(1,8),B(3,32)
(1)求f(x)的解析式;
(2)若不等式![]() +1﹣2m≥0在x∈(﹣∞,1]上恒成立,求實數m的取值范圍.
+1﹣2m≥0在x∈(﹣∞,1]上恒成立,求實數m的取值范圍.
【答案】解:(1)把點A(1,8),B(3,32)代入函數f(x)=bax , 可得![]() ,求得
,求得![]() ,∴f(x)=42x .
,∴f(x)=42x .
(2)不等式![]() +1﹣2m≥0,即 m≤
+1﹣2m≥0,即 m≤![]() [
[![]() ]2+
]2+![]()
![]() +
+![]() .
.
令t=![]() ,則 m≤
,則 m≤![]() t2+
t2+![]() t+
t+![]() .
.
記g(t)=![]() t2+
t2+![]() t+
t+![]() =
=![]() (t+
(t+![]() )2+
)2+![]() ,由x∈(﹣∞,1],可得t≥
,由x∈(﹣∞,1],可得t≥![]() .
.
故當t=![]() 時,函數g(t)取得最小值為
時,函數g(t)取得最小值為![]() .
.
由題意可得,m≤g(t)min , ∴m≤![]() .
.
【解析】(1)把點A(1,8),B(3,32)代入函數f(x)=bax , 求得a、b的值,可得f(x)的解析式.
(2)不等式即 m≤![]() [
[![]() ]2+
]2+![]()
![]() +
+![]() , 令t=
, 令t=![]() , 則 m≤
, 則 m≤![]() t2+
t2+![]() t+
t+![]() . 利用二次函數的性質求得g(t)=
. 利用二次函數的性質求得g(t)=![]() t2+
t2+![]() t+
t+![]() 的最小值,可得m的范圍.
的最小值,可得m的范圍.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,ABCD﹣A1B1C1D1是正方體,E,F,G,H,M,N分別是所在棱的中點,則下列結論錯誤的有
①GH和MN是平行直線;GH和EF是相交直線
②GH和MN是平行直線;MN和EF是相交直線
③GH和MN是相交直線;GH和EF是異面直線
④GH和EF是異面直線;MN和EF也是異面直線.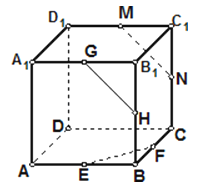
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點O(0,0),A(3,0),動點P到定點O距離與到定點A的距離的比值是![]() .
.
(Ⅰ)求動點P的軌跡方程,并說明方程表示的曲線;
(Ⅱ)當λ=4時,記動點P的軌跡為曲線D.F,G是曲線D上不同的兩點,對于定點Q(﹣3,0),有|QF||QG|=4.試問無論F,G兩點的位置怎樣,直線FG能恒和一個定圓相切嗎?若能,求出這個定圓的方程;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名高二文科生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班進行教改實驗.為了了解教學效果,期末考試后,陳老師對甲、乙兩個班級的學生成績進行統計分析,畫出頻率分布直方圖(如下圖).記成績不低于90分者為“成績優秀”.
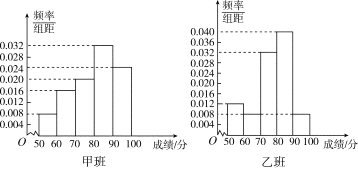
(Ⅰ)根據頻率分布直方圖填寫下面2×2列聯表;
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
(Ⅱ)判斷能否在犯錯誤的概率不超過0.05的前提下認為:“成績優秀”與教學方式有關?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數y=f(x)同時滿足:(ⅰ)對于定義域內的任意x,恒有f(x)+f(﹣x)=0;(ⅱ)對于定義域內的任意x1 , x2 , 當x1≠x2時,恒有![]() , 則稱函數f(x)為“二維函數”.現給出下列四個函數:
, 則稱函數f(x)為“二維函數”.現給出下列四個函數:
①f(x)=![]()
②f(x)=﹣x3+x
③![]()
④![]()
其中能被稱為“二維函數”的有 (寫出所有滿足條件的函數的序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com