
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線的斜率;
處的切線的斜率;
(2)當![]() 時,求函數
時,求函數![]() 的單調區間與極值.
的單調區間與極值.
【答案】(1) ![]() ;(2)當
;(2)當![]() 時,
時,![]() 在
在![]() 內是增函數,在
內是增函數,在![]() 內是減函數,函數
內是減函數,函數![]() 的極大值為
的極大值為![]() ,函數
,函數![]() 的極小值為
的極小值為![]() ;當
;當![]() 時,
時,![]() 在
在![]() 內是增函數,在
內是增函數,在![]() 內是減函數,函數
內是減函數,函數![]() 的極大值為
的極大值為![]() ,函數
,函數![]() 在
在![]() 處取得極小值
處取得極小值![]() ,且
,且![]() .
.
【解析】
試題分析:(1) 當![]() 時,
時, ![]() 求
求![]() 即可;(2)由
即可;(2)由![]() 得
得![]() ,或
,或![]() ,分
,分![]() 與
與![]() 討論兩根的大小,列表求單調區間與極值即可.
討論兩根的大小,列表求單調區間與極值即可.
試題解析: (1)當![]() 時,
時,![]() 故
故![]() .
.
所以曲線![]() 在點
在點![]() 處的切線的斜率為
處的切線的斜率為![]()
(2)解:![]() .
.
令![]() ,解得
,解得![]() ,或
,或![]() .由
.由![]() 知,
知,![]() .
.
以下分兩種情況討論:
若![]() ,則
,則![]() .當
.當![]() 變化時,
變化時,![]() 的變化情況如下表:
的變化情況如下表:

所以![]() 在
在![]() 內是增函數,在
內是增函數,在![]() 內是減函數.
內是減函數.
函數![]() 在
在![]() 處取得極大值
處取得極大值![]() ,且
,且![]() .
.
函數![]() 在
在![]() 處取得極小值
處取得極小值![]() ,且
,且![]() .
.
若![]() ,則
,則![]() ,當
,當![]() 變化時,
變化時,![]() 的變化情況如下表:
的變化情況如下表:

所以![]() 在
在![]() 內是增函數,在
內是增函數,在![]() 內是減函數.
內是減函數.
函數![]() 在
在![]() 處取得極小值
處取得極小值![]() ,且
,且![]() ,
,
函數![]() 在
在![]() 處取得極大值
處取得極大值![]() ,且
,且![]() .
.


科目:高中數學 來源: 題型:
【題目】已知直線![]() (
(![]() ).
).
(1)證明:直線![]() 過定點;
過定點;
(2)若直線不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 軸負半軸于
軸負半軸于![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,△
,△![]() 的面積為
的面積為![]() (
(![]() 為坐標原點),求
為坐標原點),求![]() 的最小值,并求此時直線
的最小值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點A處下山至C處有兩種路徑.一種是從A沿直線步行到C,另一種是先從A沿索道乘纜車到B,然后從B沿直線步行到C.現有甲、乙兩位游客從A處下山,甲沿AC勻速步行,速度為50m/min.在甲出發2min后,乙從A乘纜車到B,在B處停留1min后,再從B勻速步行到C.假設纜車勻速直線運動的速度為130m/min,山路AC長為1260m,經測量,![]() ,
,![]() .
.
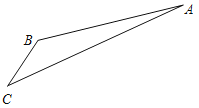
(Ⅰ)問乙出發多少分鐘后,乙在纜車上與甲的距離最短?
(Ⅱ)為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() 分鐘,乙步行的速度應控制在什么范圍內?
分鐘,乙步行的速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為1的等邊三角形ABC中,D,E分別是AB,AC邊上的點,AD=AE,F是BC的中點,AF與DE交于點G,將△ABF沿AF折起,得到如圖2所示的三棱錐A﹣BCF,其中BC=![]() .
.
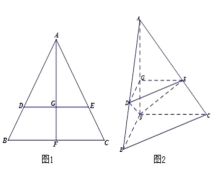
(Ⅰ)證明:DE∥平面BCF;
(Ⅱ)證明:CF⊥平面ABF;
(Ⅲ)當AD=![]() 時,求三棱錐F﹣DEG的體積.
時,求三棱錐F﹣DEG的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() 是圓
是圓![]()
![]() 上的任意一點,線段
上的任意一點,線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 交于點
交于點![]() .
.
(Ⅰ)求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)若直線![]() 與點
與點![]() 的軌跡有兩個不同的交點
的軌跡有兩個不同的交點![]() 和
和![]() ,且原點
,且原點![]() 總在以
總在以![]() 為直徑的圓的內部,求實數
為直徑的圓的內部,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知國家某5A級大型景區對擁擠等級與每日游客數量![]() (單位:百人)的關系有如下規定:當
(單位:百人)的關系有如下規定:當![]()
![]() 時,擁擠等級為“優”;當
時,擁擠等級為“優”;當![]()
![]() 時,擁擠等級為“良”;當
時,擁擠等級為“良”;當![]()
![]() 時,擁擠等級為“擁擠”;當
時,擁擠等級為“擁擠”;當![]()
![]() 時,擁擠等級為“嚴重擁擠”。該景區對6月份的游客數量作出如圖的統計數據:
時,擁擠等級為“嚴重擁擠”。該景區對6月份的游客數量作出如圖的統計數據:
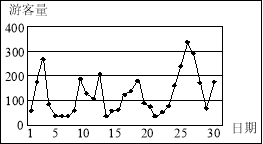
(Ⅰ)下面是根據統計數據得到的頻率分布表,求出![]() 的值,并估計該景區6月份游客人數的平均值(同一組中的數據用該組區間的中點值作代表);
的值,并估計該景區6月份游客人數的平均值(同一組中的數據用該組區間的中點值作代表);
游客數量 (單位:百人) |
|
|
|
|
天數 |
|
|
|
|
頻率 |
|
|
|
|
(Ⅱ)某人選擇在6月1日至6月5日這5天中任選2天到該景區游玩,求他這2天遇到的游客擁擠等級均為“優”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=si n![]() -2cos2
-2cos2![]() +1.
+1.
(1)求f(x)的最小正周期;
(2)若函數y=f(x)與y=g(x)的圖象關于直線x=1對稱,求當x∈![]() 時,y=g(x)的最大值.
時,y=g(x)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,點
,點![]() (
(![]() )在直線y = x上,
)在直線y = x上,
(Ⅰ)計算a2,a3,a4的值;
(Ⅱ)令bn=an+1﹣an﹣1,求證:數列{bn}是等比數列;
(Ⅲ)設Sn、Tn分別為數列{an}、{bn}的前n項和,是否存在實數λ,使得數列![]() 為等差數列?若存在,試求出λ的值;若不存在,請說明理由.
為等差數列?若存在,試求出λ的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com