
(本題滿分14分)已知函數f (x)=lnx,g(x)=ex.
(I)若函數φ (x) = f (x)- ,求函數φ (x)的單調區間;
,求函數φ (x)的單調區間;
(Ⅱ)設直線l為函數 y=f (x) 的圖象上一點A(x0,f (x0))處的切線.證明:在區間(1,+∞)上存在唯一的x0,使得直線l與曲線y=g(x)相切.
注:e為自然對數的底數.
解:(Ⅰ) 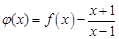
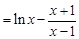 ,
,
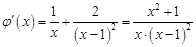 . 2分
. 2分
∵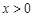 且
且 ,
,
∴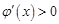
∴函數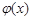 的單調遞增區間為
的單調遞增區間為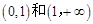 .··············· 4分
.··············· 4分
(Ⅱ)∵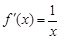 ,∴
,∴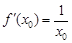 ,
,
∴ 切線 的方程為
的方程為 , http:// /
, http:// /
即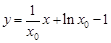 , ① ······················ 6分
, ① ······················ 6分
設直線 與曲線
與曲線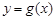 相切于點
相切于點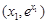 ,
,
∵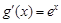 ,∴
,∴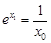 ,∴
,∴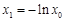 .················· 8分
.················· 8分
∴直線 也為
也為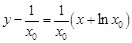 ,
,
即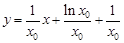 , ②······················· 9分
, ②······················· 9分
由①②得 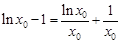 ,
,
∴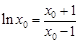 .···························· 11分
.···························· 11分
下證:在區間(1,+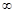 )上
)上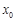 存在且唯一.
存在且唯一.
由(Ⅰ)可知,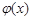
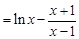 在區間
在區間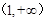 上遞增.
上遞增.
又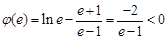 ,
,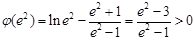 ,······ 13分
,······ 13分
結合零點存在性定理,說明方程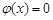 必在區間
必在區間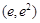 上有唯一的根,這個根就是所求的唯一
上有唯一的根,這個根就是所求的唯一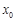 .
.
故結論成立.
【解析】略


科目:高中數學 來源:2012-2013學年吉林省高三第一次月考文科數學試卷(解析版) 題型:解答題
(本題滿分14分)已知函數
(1)若 ,求x的值;
,求x的值;
(2)若 對于
對于 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
(本題滿分14分)
已知橢圓 :
: 的離心率為
的離心率為 ,過坐標原點
,過坐標原點 且斜率為
且斜率為 的直線
的直線 與
與 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若動圓 與橢圓
與橢圓 和直線
和直線 都沒有公共點,試求
都沒有公共點,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
((本題滿分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
(1)當x=2時,求證:BD⊥EG ;
(2)若以F、B、C、D為頂點的三棱錐的體積記為 ,
,
求 的最大值;
的最大值;


(3)當 取得最大值時,求二面角D-BF-C的余弦值.
取得最大值時,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com