
【題目】在平面四邊形ABCD中, AB=2,BD=![]() ,AB⊥BC,∠BCD=2∠ABD,△ABD的面積為2.
,AB⊥BC,∠BCD=2∠ABD,△ABD的面積為2.

(1)求AD的長;
(2)求△CBD的面積.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用面積公式可以求出sin∠ABD的值,利用同角三角函數的關系求出cos∠ABD的值,利用余弦定理,求出AD的長;
(2)利用AB⊥BC,可以求出以sin∠CBD的大小,利用∠BCD=2∠ABD,可求出sin∠BCD
的大小,通過角之間的關系可以得到所以△CBD為等腰三角形,利用正弦定理,可求出CD的大小,最后利用面積公式求出△CBD的面積.
(1)由已知![]() =
=![]() AB·BD·sin∠ABD=
AB·BD·sin∠ABD=![]() ×2×
×2×![]() ×sin∠ABD=2,
×sin∠ABD=2,
可得sin∠ABD=![]() ,又∠ABD∈
,又∠ABD∈![]() ,所以cos∠ABD=
,所以cos∠ABD=![]() ,
,
在△ABD中,由余弦定理AD2=AB2+BD2-2·AB·BD·cos∠ABD,
可得AD2=5,所以AD=![]() .
.
(2)由AB⊥BC,得∠ABD+∠CBD=![]() ,所以sin∠CBD=cos∠ABD=
,所以sin∠CBD=cos∠ABD=![]() ,
,
又∠BCD=2∠ABD,所以sin∠BCD=2sin∠ABD·cos∠ABD=![]() ,
,
∠BDC=π-∠CBD-∠BCD=π-![]() -2∠ABD=
-2∠ABD=![]() -∠ABD=∠CBD,
-∠ABD=∠CBD,
所以△CBD為等腰三角形,即CB=CD,在△CBD中,由正弦定理![]() ,得CD
,得CD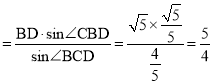 ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】若二次函數f(x)滿足f(x+1)﹣f(x)=4x+6,且f(0)=3.
(Ⅰ)求f(x)的解析式;
(Ⅱ)設g(x)=f(x)+(a﹣2)x2+(2a+2)x,g(x)在[﹣2,+∞)單調遞增,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正六棱錐被過棱錐高的中點且平行于底的平面所截,得到正六棱臺和較小的棱錐.

(1)求大棱錐、小棱錐、棱臺的側面積之比;
(2)若大棱錐的側棱長為![]() ,小棱錐的底面邊長為
,小棱錐的底面邊長為![]() ,求截得的棱臺的側面積與全面積.
,求截得的棱臺的側面積與全面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集為R,集合A={x|-3<x<4},B={x|1≤x≤10}.
(1)求A∪B,A∩(RB);
(2)已知集合C={x|2a-1≤x≤a+1},若C∩A=C,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為考查某種疫苗預防疾病的效果,進行動物實驗,得到統計數據如下:
未發病 | 發病 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現從所有試驗動物中任取一只,取到“注射疫苗”動物的概率為![]() .
.
(1)求![]() 列聯表中的數據
列聯表中的數據![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)判斷疫苗是否有效?
(3)能夠有多大把握認為疫苗有效?
(參考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,若點
,若點![]() 與橢圓左焦點構成的直線的斜率為
與橢圓左焦點構成的直線的斜率為![]() 與右焦點構成的直線的斜率為
與右焦點構成的直線的斜率為![]() ,且
,且![]() ;
;
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() 與
與![]() 軸的交點為
軸的交點為![]() ,
,![]() 為橢圓
為橢圓![]() 的中心,點
的中心,點![]() 在橢圓上,且
在橢圓上,且![]() ,若
,若![]() ,求直線
,求直線![]() 的方程
的方程
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
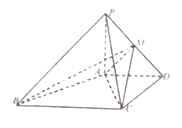
(1)求證:![]() ;
;
(2)在線段![]() 上,是否存在一點
上,是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ,如果存在,求
,如果存在,求![]() 與平面
與平面![]() 所成角的正弦值,如果不存在,請說明理由.
所成角的正弦值,如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com