Question

【題目】在平行四邊形ABCD中，E，G分別是BC，DC上的點且 =3 ， =3 ，DE與BG交于點O．
（1）求| |：| |；
（2）若平行四邊形ABCD的面積為21，求△BOC的面積．

Answer 1

【答案】
（1）解：由于D、O、E共線，故有 =λ =λ（ ﹣ ）．

∵B、O、G共線，∴ =m +（1﹣m） =m（﹣ ）+（1﹣m）（ ）

=﹣ m +（1﹣m）（ ﹣ ）= + ，

∴ = + ，

∴λ（ ﹣ ）= + ，

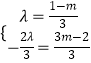∴ ，求得λ= ，

可得| |：| |=

（2）解：由（1）可得△BOC 與△BDC的高之比 = ，∴△BOC 與△BDC的面積之比為 = ，

∴S△BOC= S△BDC= =

【解析】（1）由D、O、E共線，故有 =λ =λ（ ﹣ ）．再由 B、O、G共線，求得 = + ，再利用平面向量基本定理求得λ 的值，即可得到結論．（2）由（1）可得 = ，可得 = ，再根據(jù)S△BOC= S△BDC ， 計算求得結果．
【考點精析】根據(jù)題目的已知條件，利用正弦定理的定義的相關知識可以得到問題的答案，需要掌握正弦定理:．