已知向量a=(-2,3,2),b=(1,-5,-1),則ma+b與2a-3b相互垂直的充要條件為 .
【答案】
分析:判斷向量垂直的方法是兩向量的數量積為零,可以把向量的坐標代入也可以直接計算ma+b與2a-3b的數量積,但此題用后一種方法比較好.
解答:解:∵(ma+b)(2a-3b)=0
∴2ma
2-3mb+2ab-3b=0
又∵a
2=17,b
2=27,ab=-19
∴代入可得
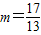
∴ma+b與2a-3b相互垂直的充要條件為
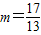
.
點評:空間向量在高考中沒有直接考查只是借助于立體幾何進行考查,因此空間向量只是一種解題工具.
