
如圖示,在底面為直角梯形的四棱椎P ABCD中,AD//BC,ÐABC= 900, PA^平面ABCD,PA= 4,AD= 2,AB=2 ,BC = 6.
,BC = 6.
(1)求證:BD^平面PAC ;
(2)求二面角A—PC—D的正切值;
(3)求點D到平面PBC的距離.
(1)見解析;(2)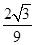 ;(3)
;(3)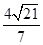
解析試題分析:(1)三角形AOB中,由勾股定理得:BO^AC,即:BD^AC, 又BD^PA,ACÇ PA=A,由線面垂直判定定理可得BD^平面PAC;(2)先作出二面角的平面角,然后在直角三角形中求出正切值;(3)利用等積法,由VD—PBC = VP—BDC即可求出點D到平面PBC的距離.
試題解析:解:(1)令BD與AC相交于點O,不難求得:AC=4 ,BD= 4
,BD= 4
由DAOD~DBOC得:BO=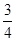 ×4= 3;AO=
×4= 3;AO= ×4
×4 =
= ;
;
\ BO2+AO2 = (3)2+( )2=" 12=" AB2
)2=" 12=" AB2
\由勾股定理得:BO^AC,即:BD^AC, 又BD^PA,ACÇ PA=A,
\ BD^平面PAC 3分
(2)由(1)知:DO^平面PAC,過O作OH^PC于H,連DH,則DH^PC
則ÐDHO就是二面角A—PC—D的平面角, DO= ×BD =
×BD = ×4="1" ,
×4="1" ,
CO=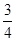 ×AC=
×AC=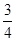 ×4
×4 =3
=3 , 由RtDPAC~RtDOHC得:
, 由RtDPAC~RtDOHC得: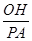 =
=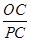 ,又PC=
,又PC=  =" 8," OH=
=" 8," OH=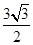 .tanÐDHO=
.tanÐDHO= 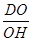 =
=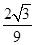 . 7分
. 7分
(3)由VD—PBC = VP—BDC可得:h=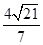 . 10分
. 10分
考點:1.線面垂直的判定;2.二面角的求法;3.點到平面的距離求法


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
(如圖,在四棱錐P﹣ABCD中,底面是邊長為2的菱形,∠BAD=60°,對角線AC與BD相交于點O,PO為四棱錐P﹣ABCD的高,且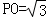 ,E、F分別是BC、AP的中點.
,E、F分別是BC、AP的中點.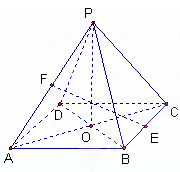
(1)求證:EF∥平面PCD;
(2)求三棱錐F﹣PCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,AB是圓的直徑,PA垂直圓所在的平面,C是圓周上的一點.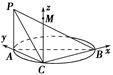
(1)求證:平面PAC⊥平面PBC;(6分)
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.(6分)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P—ABCD中,PA⊥平面ABCD,四邊形ABCD為正方形,PA=AB=4,G為PD的中點,E是AB的中點. 
(Ⅰ)求證:AG∥平面PEC;
(Ⅱ)求點G到平面PEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐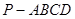 中,底面ABCD是正方形,側棱
中,底面ABCD是正方形,側棱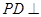 底面ABCD,
底面ABCD,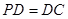 ,E是PC的中點.
,E是PC的中點.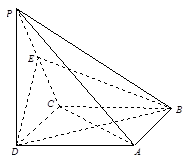
(Ⅰ)證明 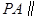 平面EDB;
平面EDB;
(Ⅱ)求EB與底面ABCD所成的角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,幾何體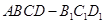 中,四邊形
中,四邊形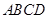 為菱形,
為菱形,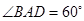 ,
,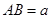 ,面
,面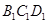 ∥面
∥面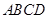 ,
,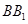 、
、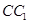 、
、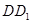 都垂直于面
都垂直于面 ,且
,且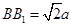 ,
,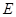 為
為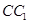 的中點,
的中點,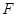 為
為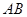 的中點.
的中點.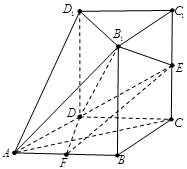
(1)求幾何體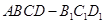 的體積;
的體積;
(2)求證: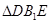 為等腰直角三角形;
為等腰直角三角形;
(3)求二面角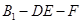 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com