【題目】已知公差不為0的等差數列{an}的前n項和為Sn ， S3＝a4＋6，且a1 ， a4 ， a13成等比數列．
（1）求數列{an}的通項公式；
（2）設bn＝2an＋1，求數列{bn}的前n項和．
【答案】
（1）設等差數列{an}的公差為d(d≠0)．
因為S3＝a4＋6，所以3a1＋ ＝a1＋3d＋6.
所以a1＝3.
因為a1，a4，a13成等比數列，
所以a1(a1＋12d)＝(a1＋3d)2，
即3(3＋12d)＝(3＋3d)2.
解得d＝2.
所以an＝2n＋1
（2）由題意bn＝22n＋1＋1，設數列{bn}的前n項和為Tn，cn＝22n＋1，
＝4(n∈N*)，所以數列{cn}為以8為首項，4為公比的等比數列．
所以Tn＝ ＋n＝ ＋n.
【解析】本題考查等差數列和等比數列的通項公式，解題時要認真審題，注意對數性質的靈活運用．
【考點精析】掌握等比數列的前n項和公式是解答本題的根本，需要知道前
項和公式：
．
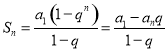科目：高中數學 來源： 題型：
【題目】某工廠從一批產品中隨機抽取20件進行檢測，如圖是根據抽樣檢測后的產品凈重（單位：克）數據的頻率分布直方圖，其中產品凈重的范圍是[140，200]，樣本數據分組為[140，150），[150，160），[160，170），[170，180），[180，190），[190，200]．
（1）求圖中a的值；
（2）若頻率視為概率，從這批產品中有放回地隨機抽取3件，求至少有2件產品的凈重在[160，180）中的概率；
（3）若產品凈重在[150，190）為合格產品，其余為不合格產品，從這20件抽樣產品中任取2件，記X表示選到不合格產品的件數，求X的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若兩直線
的傾斜角分別為
與
，則下列四個命題中正確的是（ ）
A. 若<，則兩直線的斜率：k1 < k2 B. 若=，則兩直線的斜率：k1= k2
C. 若兩直線的斜率：k1 < k2 ，則< D. 若兩直線的斜率：k1= k2 ，則=
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=ax2﹣a﹣lnx，g（x）= 
，其中a∈R，e=2.718…為自然對數的底數．
（1）討論f（x）的單調性；
（2）證明：當x＞1時，g（x）＞0；
（3）確定a的所有可能取值，使得f（x）＞g（x）在區間（1，+∞）內恒成立．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC—A1B1C1中，AC=1，AB=
，BC=
，AA1=.
（1）求證：A1B⊥B1C；
（2）求二面角A1—B1C—B的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了展示中華漢字的無窮魅力，傳遞傳統文化，提高學習熱情，某校開展《中國漢字聽寫大會》的活動．為響應學校號召，2（9）班組建了興趣班，根據甲、乙兩人近期8次成績畫出莖葉圖，如圖所示（把頻率當作概率）．
（1）求甲、乙兩人成績的平均數和中位數；
（2）現要從甲、乙兩人中選派一人參加比賽，從統計學的角度，你認為派哪位學生參加比較合適？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在公園游園活動中，有這樣一個游戲項目：甲箱子里裝有3個白球和2個黑球，乙箱子里裝有1個白球和2個黑球，這些球除顏色外完全相同.每次游戲都從這兩個箱子里各隨機地摸出2個球，若摸出的白球不少于2個，則獲獎.（每次游戲結束后將球放回原箱）
（1）求在每一次游戲中獲獎的概率；
（2）在三次游戲中，記獲獎次數為
，求的概率分布和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
