
【題目】已知a∈R,函數f(x)=x2﹣2ax+5.
(1)若a>1,且函數f(x)的定義域和值域均為[1,a],求實數a的值;
(2)若不等式x|f(x)﹣x2|![]() 1對x∈[
1對x∈[![]() ,
,![]() ]恒成立,求實數a的取值范圍.
]恒成立,求實數a的取值范圍.
【答案】(1)2;(2)![]() .
.
【解析】
(1)根據f(x)的圖象開口向上,對稱軸為x=a>1,知f(x)在[1,a]上單調遞減,所以f(1)=a求解即可.
(2)將不等式x|f(x)﹣x2|![]() 1對x∈[
1對x∈[![]() ,
,![]() ]恒成立,去絕對值轉化為a
]恒成立,去絕對值轉化為a![]() 且a
且a![]() 在x∈[
在x∈[![]() ,
,![]() ]恒成立,分別令g(x)
]恒成立,分別令g(x)![]() ,x∈[
,x∈[![]() ,
,![]() ],用二次函數求其最大值,令h(x)
],用二次函數求其最大值,令h(x)![]() ,x∈[
,x∈[![]() ,
,![]() ],求其最小值即可.
],求其最小值即可.
(1)∵f(x)的圖象開口向上,對稱軸為x=a>1,
∴f(x)在[1,a]上單調遞減,
∴f(1)=a,即6﹣2a=a,解得a=2..
(2)不等式x|f(x)﹣x2|![]() 1對x∈[
1對x∈[![]() ,
,![]() ]恒成立,
]恒成立,
即x|2ax﹣5|![]() 1對x∈[
1對x∈[![]() ,
,![]() ]恒成立,
]恒成立,
故a![]() 且a
且a![]() 在x∈[
在x∈[![]() ,
,![]() ]恒成立,
]恒成立,
令g(x)![]() ,x∈[
,x∈[![]() ,
,![]() ],
],
所以g(x)max=g(![]() )
)![]() ,
,
所以![]() .
.
令h(x)![]() ,x∈[
,x∈[![]() ,
,![]() ],
],
所以h(x)min=h(![]() )=7,
)=7,
所以![]() .
.
綜上:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在正方形![]() 中,
中,![]() ,
,![]() 分別為棱
分別為棱![]() 和棱
和棱![]() 的中點,則下列說法正確的是( )
的中點,則下列說法正確的是( )
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() 截正方體所得截面為等腰梯形
截正方體所得截面為等腰梯形
C.![]() 平面
平面![]() D.異面直線
D.異面直線![]() 與
與![]() 所成的角為60°
所成的角為60°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】推進垃圾分類處理,是落實綠色發展理念的必然選擇,也是打贏污染防治攻堅戰的重要環節.為了解居民對垃圾分類的了解程度某社區居委會隨機抽取1000名社區居民參與問卷測試,并將問卷得分繪制頻率分布表如表:
得分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男性人數 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人數 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)從該社區隨機抽取一名居民參與問卷測試試估計其得分不低于60分的概率:
(2)將居民對垃圾分類的了解程度分為“比較了解”(得分不低于60分)和“不太了解”(得分低于60)兩類,完成2×2列聯表,并判斷是否有95%的把握認為“居民對垃圾分類的了解程度”與“性別”有關?
不太了解 | 比較了解 | 合計 | |
男性 | |||
女性 | |||
合計 |
(3)從參與問卷測試且得分不低于80分的居民中,按照性別進行分層抽樣,共抽取10人,現從這10人中隨機抽取3人作為環保宣傳隊長,設3人中男性隊長的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:![]() .
.
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列是合情推理的是( )
①由正三角形的性質類比出正三棱錐的有關性質;
②由正方形矩形的內角和是![]() ,歸納出所有四邊形的內角和都是;
,歸納出所有四邊形的內角和都是;
③三角形內角和是![]() ,四邊形內角和是
,四邊形內角和是![]() ,五邊形內角和是
,五邊形內角和是![]() ,由此得出凸
,由此得出凸![]() 邊形內角和是
邊形內角和是![]() ;
;
④小李某次數學考試成績是90分,由此推出小李的全班同學這次數學考試的成績都是90分.
A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的多面體ABCDE中,已知ABCD是邊長為2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.
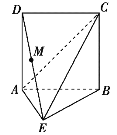
(1)若M是DE的中點,試在AC上找一點N,使得MN∥平面ABE,并給出證明;
(2)求多面體ABCDE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓上一點與橢圓的兩個焦點構成的三角形周長為
,且橢圓上一點與橢圓的兩個焦點構成的三角形周長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以
兩點,且以![]() 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com