
【題目】網約車的興起豐富了民眾出行的選擇,為民眾出行提供便利的同時也解決了很多勞動力的就業問題,據某著名網約車公司“滴滴打車”官網顯示,截止目前,該公司已經累計解決退伍軍人轉業為兼職或專職司機三百多萬人次,梁某即為此類網約車司機,據梁某自己統計某一天出車一次的總路程數可能的取值是20、22、24、26、28、![]() ,它們出現的概率依次是
,它們出現的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求這一天中梁某一次行駛路程X的分布列,并求X的均值和方差;
(2)網約車計費細則如下:起步價為5元,行駛路程不超過![]() 時,租車費為5元,若行駛路程超過
時,租車費為5元,若行駛路程超過![]() ,則按每超出
,則按每超出![]() (不足
(不足![]() 也按
也按![]() 計程)收費3元計費.依據以上條件,計算梁某一天中出車一次收入的均值和方差.
計程)收費3元計費.依據以上條件,計算梁某一天中出車一次收入的均值和方差.
科目:高中數學 來源: 題型:
【題目】中國第一高摩天輪“南昌之星摩天輪”高度為![]() ,其中心
,其中心![]() 距地面
距地面![]() ,半徑為
,半徑為![]() ,若某人從最低點
,若某人從最低點![]() 處登上摩天輪,摩天輪勻速旋轉,那么此人與地面的距離將隨時間
處登上摩天輪,摩天輪勻速旋轉,那么此人與地面的距離將隨時間![]() 變化,
變化,![]() 后達到最高點,從登上摩天輪時開始計時.
后達到最高點,從登上摩天輪時開始計時.
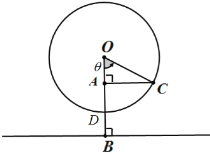
(1)求出人與地面距離![]() 與時間
與時間![]() 的函數解析式;
的函數解析式;
(2)從登上摩天輪到旋轉一周過程中,有多長時間人與地面距離大于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知具有線性相關關系的兩個變量![]() 之間的幾組數據如下表所示:
之間的幾組數據如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并估計當
,并估計當![]() 時,
時, ![]() 的值;
的值;
(2)將表格中的數據看作五個點的坐標,則從這五個點中隨機抽取2個點,求恰有1個點落在直線![]() 右下方的概率.
右下方的概率.
參考公式: 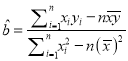 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只藥用昆蟲的產卵數y與一定范圍內的溫度x有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
溫度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
產卵數y/個 | 6 | 11 | 20 | 27 | 57 | 77 |
經計算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,線性回歸模型的殘差平方和
,線性回歸模型的殘差平方和![]() ,e8.0605≈3167,其中xi, yi分別為觀測數據中的溫度和產卵數,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分別為觀測數據中的溫度和產卵數,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用線性回歸模型,求y關于x的回歸方程![]() =
=![]() x+
x+![]() (精確到0.1);
(精確到0.1);
(Ⅱ)若用非線性回歸模型求得y關于x的回歸方程為![]() =0.06e0.2303x,且相關指數R2=0.9522.
=0.06e0.2303x,且相關指數R2=0.9522.
( i )試與(Ⅰ)中的回歸模型相比,用R2說明哪種模型的擬合效果更好.
( ii )用擬合效果好的模型預測溫度為35C時該種藥用昆蟲的產卵數(結果取整數).
附:一組數據(x1,y1), (x2,y2), ...,(xn,yn ), 其回歸直線![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估計為
的斜率和截距的最小二乘估計為

![]() =
=![]()
![]() ;相關指數R2=
;相關指數R2= .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4.
的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 是橢圓
是橢圓![]() 的左頂點,經過左焦點
的左頂點,經過左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,求
兩點,求![]() 與
與![]() 的面積之差的絕對值的最大值.(
的面積之差的絕對值的最大值.(![]() 為坐標原點)
為坐標原點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲、乙兩種產品,銷售利潤分別為2千元/件、1千元/件.甲、乙兩種產品都需要在![]() 兩種設備上加工,生產一件甲產品需用
兩種設備上加工,生產一件甲產品需用![]() 設備2小時,
設備2小時, ![]() 設備6小時;生產一件乙產品需用
設備6小時;生產一件乙產品需用![]() 設備3小時,
設備3小時, ![]() 設備1小時.
設備1小時. ![]() 兩種設備每月可使用時間數分別為480小時、960小時,若生產的產品都能及時售出,則該企業每月利潤的最大值為( )
兩種設備每月可使用時間數分別為480小時、960小時,若生產的產品都能及時售出,則該企業每月利潤的最大值為( )
A. 320千元 B. 360千元 C. 400千元 D. 440千元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com