Question

22.已知復數z₀＝l－mi（m>0），z=x+yi和w=x′+y′i.其中x，y，x′,y′均為實數.i為虛數單位，且對于任意復數z，有w=·，.

（1）試求m的值，并分別寫出x′和y′用x、y表示的關系式；

（2）將（x，y）作為點P的坐標，（x′，y′）作為點Q的坐標，上述關系式可以看作是坐標平面上點的一個變換：它將平面上的點P變到這一平面上的點Q.

當點P在直線y=x+1上移動時，試求點P經該變換后得到的點Q的軌跡方程.

（3）是否存在這樣的直線：它上面的任一點經上述變換后得到的點仍在c 該直線上？若存在，試求出所有這些直線；若不存在，則說明理由.

Answer 1

22.解：

（1）由題設，｜w｜=｜｜=｜z₀｜｜z｜=2｜z｜，

∴｜z₀｜=2，

于是由1+m²=4，且m>0，得m=.　　　　　　　　　　

因此由，

得關系式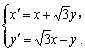　　　　　　　　　　　　　　　　

 

（2）設點P（x，y）在直線y=x+1上，則其經變換后的點Q（，）滿足

　　　　　　　　　　　　　　　  

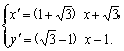
消去x，得，

故點Q的軌跡方程為.　　　　　　

 

（3）假設存在這樣的直線，∵平行坐標軸的直線顯然不滿足條件，

∴所求直線可設為y=kx+b（k≠0）.　　　　　　　　　　　

解法一：∵該直線上的任一點P（x，y），其經變換后得到的點Q（x+，）仍在該直線上，

∴，

即－（）y=（k－）x+b.　　　　　　　　　　

當b≠0時，方程組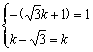無解，

故這樣的直線不存在.　　　　　　　　　　　　　　　　

當b=0時，由，

得，

解得或，

故這樣的直線存在，其方程為y=.　　　

解法二：取直線上一點P（），其經變換后的點Q（）仍在該直線上，

∴，

得b=0，　　 　　　　　　　　　　　　　　　　　　　

故所求直線為y=kx，取直線上一點P（1，k），其經變換后得到的點Q（1+，）仍在該直線上，

∴，　 　　　　　　　　　　　　　

即，

得或，

故這樣的直線存在，其方程為y＝或y=.