
定義在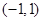 上的函數
上的函數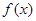 滿足:對任意
滿足:對任意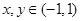 ,
,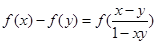 恒成立.有下列結論:①
恒成立.有下列結論:①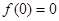 ;②函數
;②函數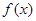 為
為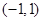 上的奇函數;③函數
上的奇函數;③函數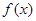 是定義域內的增函數;④若
是定義域內的增函數;④若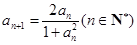 ,且
,且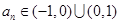 ,則數列
,則數列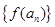 為等比數列.
為等比數列.
其中你認為正確的所有結論的序號是 .
①②④
【解析】
試題分析:因為已知中,函數滿足對任意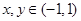 ,
,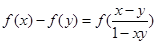 恒成立
恒成立
那么可知f(0)-f(0)=f(0),故有f(0)=0,故命題1正確。
命題2中,令0=x,y=x則f(0)-f(x)=f(-x),f(-x)+f(x)=0,可知為奇函數。
故正確。
命題3中,令x=1,y=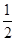 .那么可知得到f(
.那么可知得到f(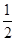 )=0,顯然不符合單調函數定義,錯誤。
)=0,顯然不符合單調函數定義,錯誤。
命題4總,由于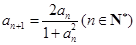 ,且
,且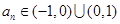 ,則數列
,則數列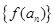 為等比數列,故成立。正確的序號為①②④
為等比數列,故成立。正確的序號為①②④
考點:本試題主要是考查了函數的單調性和數列的綜合運用。
點評:解決該試題的關鍵是利用抽象函數的表達式,進行合理的賦值,然后結合函數的奇偶性的性質很單調性的性質來求解分析得到結論。體現了抽象函數的賦值思想的運用,屬于中檔題。


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源:2014屆湖北穩派教育高三10月聯合調研考試文科數學試卷(解析版) 題型:選擇題
已知定義在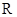 上的函數
上的函數 滿足
滿足 ,且
,且 的導函數
的導函數 在
在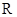 上恒有
上恒有 ,則不等式
,則不等式 的解集為( )
的解集為( )
A. 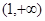 B.
B.
 C.
C.
 D.
D.
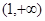
查看答案和解析>>
科目:高中數學 來源:2010屆沈陽市高三第二次模擬考試數學試卷 題型:選擇題
定義在 上的函數
上的函數 滿足:對于
滿足:對于 ,總有
,總有 ,則下列說法正確的是:( )
,則下列說法正確的是:( )
(A) 是奇函數 (B)
是奇函數 (B) 是奇函數(C)
是奇函數(C) 是奇函數(D)
是奇函數(D) 是奇函數
是奇函數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com