
【題目】在實(shí)數(shù)集R中,我們定義的大小關(guān)系“>”為全體實(shí)數(shù)排了一個(gè)“序”.類(lèi)似地,我們?cè)趶?fù)數(shù)集C上也可以定義一個(gè)稱(chēng)為“序”的關(guān)系,記為“>”.定義如下:對(duì)于任意兩個(gè)復(fù)數(shù):![]() 當(dāng)且僅當(dāng)“
當(dāng)且僅當(dāng)“![]() ”或“
”或“![]() ”且“
”且“![]() ”.按上述定義的關(guān)系“>”,給出以下四個(gè)命題:
”.按上述定義的關(guān)系“>”,給出以下四個(gè)命題:
①若![]() ,則
,則![]() ;
;
②若![]() ,則
,則![]() ;
;
③若![]() ,則對(duì)于任意
,則對(duì)于任意![]() ;
;
④對(duì)于復(fù)數(shù)![]() ,若
,若![]() ,則
,則![]() .
.
其中所有真命題的序號(hào)為______________.
【答案】②③
【解析】
根據(jù)新定義“序”的關(guān)系,對(duì)四個(gè)命題逐一分析,由此判斷出真命題的序號(hào).
對(duì)于①,由于![]() ,所以“
,所以“![]() ”或“
”或“![]() 且
且![]() ”. 當(dāng)
”. 當(dāng)![]() ,滿(mǎn)足
,滿(mǎn)足![]() 但
但![]() ,所以①錯(cuò)誤.
,所以①錯(cuò)誤.
對(duì)于②,根據(jù)“序”的關(guān)系的定義可知,復(fù)數(shù)的“序”有傳遞性,所以②正確.
對(duì)于③,設(shè)![]() ,由
,由![]() ,所以“
,所以“![]() ”或“
”或“![]() 且
且![]() ”,可得“
”,可得“![]() ”或“
”或“![]() 且
且![]() ”,即
”,即![]() 成立,所以③正確.
成立,所以③正確.
對(duì)于④,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,故④錯(cuò)誤.
,故④錯(cuò)誤.
故答案為:②③



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() (其中a是常數(shù)).
(其中a是常數(shù)).
(1)求過(guò)點(diǎn)![]() 與曲線(xiàn)
與曲線(xiàn)![]() 相切的直線(xiàn)方程;
相切的直線(xiàn)方程;
(2)是否存在![]() 的實(shí)數(shù),使得只有唯一的正數(shù)a,當(dāng)
的實(shí)數(shù),使得只有唯一的正數(shù)a,當(dāng)![]() 時(shí)不等式
時(shí)不等式![]() 恒成立,若這樣的實(shí)數(shù)k存在,試求k,a的值;若不存在.請(qǐng)說(shuō)明理由.
恒成立,若這樣的實(shí)數(shù)k存在,試求k,a的值;若不存在.請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)橢圓![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的直線(xiàn)
的直線(xiàn)![]() ,
,![]() 分別交
分別交![]() 于不同的兩點(diǎn)
于不同的兩點(diǎn)![]() 、
、![]() ,直線(xiàn)
,直線(xiàn)![]() 恒過(guò)點(diǎn)
恒過(guò)點(diǎn)![]()
(1)證明:直線(xiàn)![]() ,
,![]() 的斜率之和為定值;
的斜率之和為定值;
(2)直線(xiàn)![]() ,
,![]() 分別與
分別與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點(diǎn),在
兩點(diǎn),在![]() 軸上是否存在定點(diǎn)
軸上是否存在定點(diǎn)![]() ,使得
,使得![]() 為定值?若存在,求出點(diǎn)
為定值?若存在,求出點(diǎn)![]() 的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
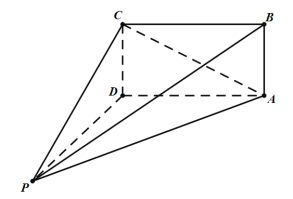
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 為正方形,且
為正方形,且![]() .若四棱錐
.若四棱錐![]() 的每個(gè)頂點(diǎn)都在球
的每個(gè)頂點(diǎn)都在球![]() 的球面上,則球
的球面上,則球![]() 的表面積的最小值為_____;當(dāng)四棱錐
的表面積的最小值為_____;當(dāng)四棱錐![]() 的體積取得最大值時(shí),二面角
的體積取得最大值時(shí),二面角![]() 的正切值為_______.
的正切值為_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直三棱柱![]() 中,底面是邊長(zhǎng)為2的等邊三角形,點(diǎn)D,E分別是
中,底面是邊長(zhǎng)為2的等邊三角形,點(diǎn)D,E分別是![]() 的中點(diǎn).
的中點(diǎn).
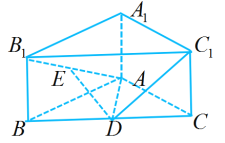
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,證明:
,證明:![]() 平面
平面![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
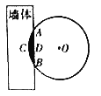
【題目】《九章算術(shù)》是我國(guó)古代數(shù)學(xué)經(jīng)典名著,其中有這樣一個(gè)問(wèn)題:“今有圓材,埋在壁中,不知大小.以鋸鋸之,深一寸,鋸道長(zhǎng)一尺.問(wèn)徑幾何?”其意為:今有-圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該木材,鋸口深一寸,鋸道長(zhǎng)-尺.問(wèn)這塊圓柱形木材的直徑是多少?現(xiàn)有長(zhǎng)為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示(陰影部分為鑲嵌在墻體內(nèi)的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌在墻體中的體積約為__________立方寸.(結(jié)果保留整數(shù))
寸,估算該木材鑲嵌在墻體中的體積約為__________立方寸.(結(jié)果保留整數(shù))
注:l丈=10尺=100寸,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]()
![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(Ⅱ)在銳角![]() 中,若
中,若![]() ,且能蓋住
,且能蓋住![]() 的最小圓的面積為
的最小圓的面積為![]() ,求
,求![]() 周長(zhǎng)的取值范圍.
周長(zhǎng)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我們?cè)谇蟾叽畏匠袒虺椒匠痰慕平鈺r(shí)常用二分法求解,在實(shí)際生活中還有三分法.比如借助天平鑒別假幣.有三枚形狀大小完全相同的硬幣,其中有一假幣(質(zhì)量較輕),把兩枚硬幣放在天平的兩端,若天平平衡,則剩余一枚為假幣,若天平不平衡,較輕的一端放的硬幣為假幣.現(xiàn)有 27 枚這樣的硬幣,其中有一枚是假幣(質(zhì)量較輕),如果只有一臺(tái)天平,則一定能找到這枚假幣所需要使用天平的最少次數(shù)為( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為推進(jìn)“千村百鎮(zhèn)計(jì)劃”,![]() 年
年![]() 月某新能源公司開(kāi)展“電動(dòng)莆田 綠色出行”活動(dòng),首批投放
月某新能源公司開(kāi)展“電動(dòng)莆田 綠色出行”活動(dòng),首批投放![]() 臺(tái)
臺(tái)![]() 型新能源車(chē)到莆田多個(gè)村鎮(zhèn),供當(dāng)?shù)卮迕衩赓M(fèi)試用三個(gè)月.試用到期后,為了解男女試用者對(duì)
型新能源車(chē)到莆田多個(gè)村鎮(zhèn),供當(dāng)?shù)卮迕衩赓M(fèi)試用三個(gè)月.試用到期后,為了解男女試用者對(duì)![]() 型新能源車(chē)性能的評(píng)價(jià)情況,該公司要求每位試用者填寫(xiě)一份性能綜合評(píng)分表(滿(mǎn)分為
型新能源車(chē)性能的評(píng)價(jià)情況,該公司要求每位試用者填寫(xiě)一份性能綜合評(píng)分表(滿(mǎn)分為![]() 分).最后該公司共收回
分).最后該公司共收回![]() 份評(píng)分表,現(xiàn)從中隨機(jī)抽取
份評(píng)分表,現(xiàn)從中隨機(jī)抽取![]() 份(其中男、女的評(píng)分表各
份(其中男、女的評(píng)分表各![]() 份)作為樣本,經(jīng)統(tǒng)計(jì)得到如下莖葉圖:
份)作為樣本,經(jīng)統(tǒng)計(jì)得到如下莖葉圖:

(1)求![]() 個(gè)樣本數(shù)據(jù)的中位數(shù)
個(gè)樣本數(shù)據(jù)的中位數(shù)![]() ;
;
(2)已知![]() 個(gè)樣本數(shù)據(jù)的平均數(shù)
個(gè)樣本數(shù)據(jù)的平均數(shù)![]() ,記
,記![]() 與
與![]() 的最大值為
的最大值為![]() .該公司規(guī)定樣本中試用者的“認(rèn)定類(lèi)型”:評(píng)分不小于
.該公司規(guī)定樣本中試用者的“認(rèn)定類(lèi)型”:評(píng)分不小于![]() 的為“滿(mǎn)意型”,評(píng)分小于
的為“滿(mǎn)意型”,評(píng)分小于![]() 的為“需改進(jìn)型”.
的為“需改進(jìn)型”.
①請(qǐng)根據(jù)![]() 個(gè)樣本數(shù)據(jù),完成下面
個(gè)樣本數(shù)據(jù),完成下面![]() 列聯(lián)表:
列聯(lián)表:
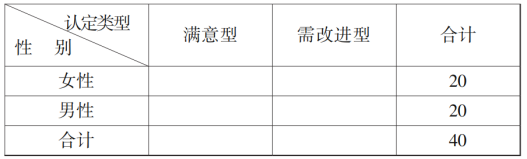
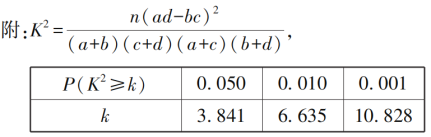
根據(jù)![]() 列聯(lián)表判斷能否有
列聯(lián)表判斷能否有![]() 的把握認(rèn)為“認(rèn)定類(lèi)型”與性別有關(guān)?
的把握認(rèn)為“認(rèn)定類(lèi)型”與性別有關(guān)?
②為做好車(chē)輛改進(jìn)工作,公司先從樣本“需改進(jìn)型”的試用者按性別用分層抽樣的方法,從中抽取8人進(jìn)行回訪(fǎng),根據(jù)回訪(fǎng)意見(jiàn)改進(jìn)車(chē)輛后,再?gòu)倪@8人中隨機(jī)抽取3人進(jìn)行二次試用,記這3人中男性人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com