
【題目】設函數![]() 是定義在
是定義在![]() 上的偶函數,且對任意的
上的偶函數,且對任意的![]() ,都有
,都有![]() .當
.當![]() 時,
時,![]() .若直線
.若直線![]() 與函數
與函數![]() 的圖象有兩個不同的公共點,則實數
的圖象有兩個不同的公共點,則實數![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
【答案】C
【解析】試題分析:解:因為函數f(x)是定義在R上的偶函數,設x∈[-1,0],則-x∈[0,1],于是f(x)=(-x)2=x2.
設x∈[1,2],則(x-2)∈[-1,0].于是,f(x)=f(x-2)=(x-2)2.
①當a=0時,聯立y="x," y=x2,解得x=0,y=0,或x=y=1,即當a=0時,即直線y=x+a與函數y=f(x)的圖象有兩個不同的公共點.
②當-2<a<0時,只有當直線y=x+a與函數f(x)=x2在區間[0,1)上相切,且與函數f(x)=(x-2)2在x∈[1,2)上僅有一個交點時才滿足條件.由f′(x)=2x=1,解得x=![]() ∴y=(
∴y=(![]() )2=
)2=![]() ,故其切點為(
,故其切點為(![]() ,
,![]() )
)
),∴a=![]() -
-![]() =-
=-![]() 由y=x-
由y=x-![]() , y=(x-2)2(1≤x<2)解之得x=
, y=(x-2)2(1≤x<2)解之得x=![]() 綜上①②可知:直線y=x+a與函數y=f(x)在區間[0,2)上的圖象有兩個不同的公共點時的a的值為0或-
綜上①②可知:直線y=x+a與函數y=f(x)在區間[0,2)上的圖象有兩個不同的公共點時的a的值為0或-![]() 又函數f(x)是定義在R上的偶函數,且對任意的x∈R,都有f(x+2)=f(x),實數a的值為
又函數f(x)是定義在R上的偶函數,且對任意的x∈R,都有f(x+2)=f(x),實數a的值為![]() 或
或![]() ,(n∈Z).故應選C.
,(n∈Z).故應選C.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人獨立地對某一技術難題進行攻關。甲能攻克的概率為![]() ,乙能攻克的概率為
,乙能攻克的概率為![]() ,丙能攻克的概率為
,丙能攻克的概率為![]() .
.
(1)求這一技術難題被攻克的概率;
(2)若該技術難題末被攻克,上級不做任何獎勵;若該技術難題被攻克,上級會獎勵![]() 萬元。獎勵規則如下:若只有1人攻克,則此人獲得全部獎金
萬元。獎勵規則如下:若只有1人攻克,則此人獲得全部獎金![]() 萬元;若只有2人攻克,則獎金獎給此二人,每人各得
萬元;若只有2人攻克,則獎金獎給此二人,每人各得![]() 萬元;若三人均攻克,則獎金獎給此三人,每人各得
萬元;若三人均攻克,則獎金獎給此三人,每人各得![]() 萬元。設甲得到的獎金數為X,求X的分布列和數學期望。(本題滿分12分)
萬元。設甲得到的獎金數為X,求X的分布列和數學期望。(本題滿分12分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市出租車收費標準如下:起步價為8元,起步里程為3 km(不超過3 km按起步價付費);超過3 km但不超過8 km時,超過部分按每千米2.15元收費;超過8 km時,超過部分按每千米2.85元收費,另每次乘坐需付燃油附加費1元.現某人乘坐一次出租車付費22.6元,則此次出租車行駛了________km.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列對應是否為集合A到集合B的函數.
(1)A=R,B={x|x>0},f:x→y=|x|;
(2)A=Z,B=Z,f:x→y=x2;
(3)A=Z,B=Z,f:x→y=![]() ;
;
(4)A={x|-1≤x≤1},B={0},f:x→y=0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學高三文科班學生共有800人參加了數學與地理的水平測試,現從中隨機抽取100人的數學與地理的水平測試成績如下表:
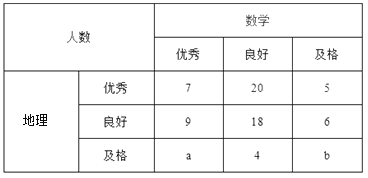
成績分為優秀、良好、及格三個等級;橫向,縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有![]() .
.
(Ⅰ)若在該樣本中,數學成績優秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求數學成績為優秀的人數比及格的人數少的概率.
,求數學成績為優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,四邊形ADEF是正方形,且BD⊥平面CDE,H是BE的中點,G是AE,DF的交點.

(1)求證:GH∥平面CDE;
(2)求證:面ADEF⊥面ABCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2014陜西理8】原命題為“若![]() 互為共軛復數,則
互為共軛復數,則![]() ”,關于逆命題,否命題,逆否命題真假性的判斷依次如下,正確的是( )
”,關于逆命題,否命題,逆否命題真假性的判斷依次如下,正確的是( )
A. 真,假,真 B. 假,假,真
C. 真,真,假 D. 假,假,假
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com