
(08年潮州市二模理)(14分)
如圖,四面體ABCD中,O、E分別是BD、BC的中點, ![]()
⑴ 求證:![]() 平面BCD;
平面BCD;
⑵ 求異面直線AB與CD所成角余弦的大小;
⑶ 求點E到平面ACD的距離.

解析:方法一:
⑴.證明:連結OC
![]() ………… 1分
………… 1分
![]() ,
,![]() . ……… 2分
. ……… 2分
在![]() 中,由已知可得
中,由已知可得![]() … 3分
… 3分
而![]() ,
, ![]() ………………… 4分
………………… 4分
![]() 即
即![]() ………………… 5分
………………… 5分
![]()
∴![]() 平面
平面![]() . …………………………… 6分
. …………………………… 6分
⑵.解:取AC的中點M,連結OM、ME、OE,由E為
BC的中點知![]() ,
,
∴ 直線OE與EM所成的銳角就是異面直線AB與CD所成的角,……………… 8分
在![]() 中,
中,![]()
![]() 是直角
是直角![]() 斜邊AC上的中線,∴
斜邊AC上的中線,∴![]() …………… 9分
…………… 9分
∴![]() , ……………………… 10分
, ……………………… 10分
∴異面直線AB與CD所成角余弦的大小為![]() . …………………………………… 11分
. …………………………………… 11分
⑶.解:設點E到平面ACD的距離為![]() .
.
![]() ,
,![]() …………………………12分
…………………………12分
在![]() 中,
中,![]() ,
,
![]() ,而
,而![]() ,
,![]() .
.
∴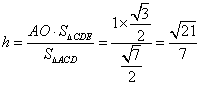 ,
,
∴點E到平面ACD的距離為![]() …………………………… 14分
…………………………… 14分

方法二:⑴.同方法一.
⑵.解:以O為原點,如圖建立空間直角坐標系,則![]()
![]()
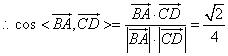 , …………… 9分
, …………… 9分
∴ 異面直線AB與CD所成角余弦的大小為![]() .…… 10分
.…… 10分
⑶.解:設平面ACD的法向量為![]() 則
則
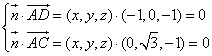 ,
,
∴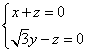 ,令
,令![]() 得
得![]() 是平面ACD的一個法向量.
是平面ACD的一個法向量.
又![]()
∴點E到平面ACD的距離 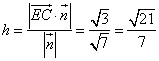 .……… ……… 14分
.……… ……… 14分



科目:高中數學 來源: 題型:
(08年潮州市二模理)(14分)已知函數![]() 的導數
的導數![]() 滿足
滿足![]() ,常數
,常數![]() 為方程
為方程![]() 的實數根.
的實數根.
⑴ 若函數![]() 的定義域為I,對任意
的定義域為I,對任意![]() ,存在
,存在![]() ,使等式
,使等式![]() =
=![]() 成立,
成立,
求證:方程![]() 不存在異于
不存在異于![]() 的實數根;
的實數根;
⑵ 求證:當![]() 時,總有
時,總有![]() 成立;
成立;
⑶ 對任意![]() ,若滿足
,若滿足![]() ,求證
,求證![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
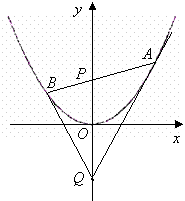
(08年潮州市二模理)(14分)如圖,過拋物線![]() 的對稱軸上任一點
的對稱軸上任一點![]() 作直線與拋物線交于A、B兩點,點Q是點P關于原點的對稱點.
作直線與拋物線交于A、B兩點,點Q是點P關于原點的對稱點.
⑴ 設點P滿足![]() (
(![]() 為實數),證明:
為實數),證明:![]() ;
;
⑵ 設直線AB的方程是![]() ,過A、B兩點的圓C與拋物線在點A處有共同的切線,求圓C的方程.
,過A、B兩點的圓C與拋物線在點A處有共同的切線,求圓C的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com