Question

求下列函數的解析式:

(1)已知f(x)=x²+2x,求f(2x+1)；

(2)已知f(－1)=x+2,求f(x)；

(3)已知f(x)－2f()=3x+2,求f(x).

Answer 1

(1)解:f(2x+1)=(2x+1)²+2(2x+1)= 4x²+8x+3.

(2)解法一:拼湊法.

f(－1)=(－1)²+4(－1)+3.

而－1≥－1.

故所求的函數f(x)=x²+4x+3(x≥－1).

解法二:換元法.

令t=－1,則t≥－1,且=t+1,

∴f(t)=(t+1)²+2(t+1)=t²+4t+3.

故所求的函數為f(x)=x²+4x+3(x≥－1).

(3)解:令t=,則x=,∴f()－2f(t)=+2,

即f()－2f(x)=+2,與原式聯立得

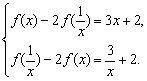
解得f(x)=－x－－2.

故所求的函數為f(x)=－x－－2.

點評:求函數解析式的常見方法:代入法、待定系數法、拼湊法、換元法、方程組法等.