與x軸,y軸以及直線4x+3y-12=0都相切的半徑最大的圓的標準方程為 .
【答案】
分析:先根據所求的圓與x軸,y軸以及直線4x+3y-12=0都相切可得到圓心到它們的距離均相等,進而可設圓心坐標為(a,b),由圓心到x軸,y軸距離即圓心的坐標可確定a=b=圓心到直線4x+3y-12=0的距離,進而可解出a=b=1或6,從而可得到答案.
解答:解:因為是與與x軸,y軸以及直線4x+3y-12=0都相切
∴圓心到它們的距離均相等
設圓心為(a,b) 圓心到x軸,y軸距離即圓心的坐標
因為距離均相等 所以a=b 則圓心到直線4x+3y-12=0的距離也等于|a|
根據點到直線的距離公式
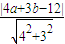
=|a|
∴a=b=1或6
則半徑最大的圓的標準方程為
(x-6)
2+(y-6)
2=36
故答案為:(x-6)
2+(y-6)
2=36
點評:本題主要考查直線與圓的位置關系和點到直線的距離.考查基礎知識的綜合運用.

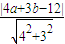 =|a|
=|a|

 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案