
【題目】在區(qū)間[0,2]上任取兩個實數a,b,則函數f(x)=x3+ax﹣b在區(qū)間[﹣1,1]上有且只有一個零點的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:由題意知本題是一個幾何概型, ∵a∈[0,2],
∴f'(x)=3x2+a≥0,
∴f(x)是增函數
若f(x)在[﹣1,1]有且僅有一個零點,
則f(﹣1)f(1)≤0
∴(﹣1﹣a﹣b)(1+a﹣b)≤0,
即(1+a+b)(1+a﹣b)≥0 ![]() =
= ![]() 11
11
由線性規(guī)劃內容知全部事件的面積為2×2=4,滿足條件的面積4﹣ ![]() =
= ![]()
∴P= ![]() =
= ![]()
故選D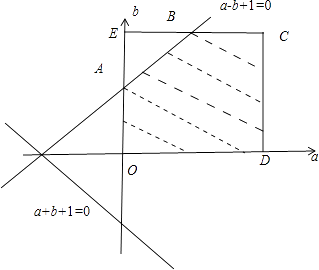
【考點精析】掌握幾何概型和函數的零點是解答本題的根本,需要知道幾何概型的特點:1)試驗中所有可能出現的結果(基本事件)有無限多個;2)每個基本事件出現的可能性相等;函數的零點就是方程的實數根,亦即函數的圖象與軸交點的橫坐標.即:方程有實數根,函數的圖象與坐標軸有交點,函數有零點.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣kx+k.
(Ⅰ)若f(x)≥0有唯一解,求實數k的值;
(Ⅱ)證明:當a≤1時,x(f(x)+kx﹣k)<ex﹣ax2﹣1.
(附:ln2≈0.69,ln3≈1.10, ![]() ,e2≈7.39)
,e2≈7.39)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x+ ![]() |+|x﹣2m|(m>0). (Ⅰ)求證:f(x)≥8恒成立;
|+|x﹣2m|(m>0). (Ⅰ)求證:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】參與舒城中學數學選修課的同學對某公司的一種產品銷量與價格進行了統計,得到如下數據和散點圖.
定價x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年銷量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

參考數據:
![]() ,
,
![]() .
.
(1)根據散點圖判斷y與x,z與x哪一對具有較強的線性相關性(給出判斷即可,不必說明理由)?
(2)根據(1)的判斷結果及數據,建立y關于x的回歸方程(方程中的系數均保留兩位有效數字).
(3)當定價為150元/千克時,試估計年銷量.
附:對于一組數據(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回歸直線![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估計分別為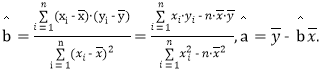
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應國建“精準扶貧,產業(yè)扶貧”的戰(zhàn)略,某市面向全國征召《扶貧政策》義務宣傳志愿者,從年齡在[20,45]的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示 
(1)求圖中x的值
(2)在抽出的100名志愿者中按年齡采取分層抽樣的方法抽取10名參加中心廣場的宣傳活動,再從這10名志愿者中選取3名擔任主要負責人,記這3名志愿者中“年齡低于35歲”的人數為Y,求Y的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ea(x﹣1)﹣ax2 , a為不等于零的常數.
(Ⅰ)當a<0時,求函數f′(x)的零點個數;
(Ⅱ)若對任意x1 , x2 , 當x1<x2時,f(x2)﹣f(x1)>a( ![]() ﹣2x1)(x2﹣x1)恒成立,求實數a的取值范圍.
﹣2x1)(x2﹣x1)恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】整改校園內一塊長為15 m,寬為11 m的長方形草地(如圖A),將長減少1 m,寬增加1 m(如圖B).問草地面積是增加了還是減少了?假設長減少x m,寬增加x m(x>0),試研究以下問題:

x取什么值時,草地面積減少?
x取什么值時,草地面積增加?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com