
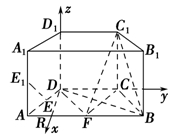
如圖,在直四棱柱ABCD-A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分別是棱AD,AA1,AB的中點.
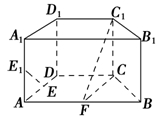
(1)證明:直線EE1∥平面FCC1;
(2)求二面角B-FC1-C的余弦值.
(1)見解析(2)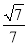
【解析】(1)證明
法一 取A1B1的中點F1,連接FF1,C1F1,由于FF1∥BB1∥CC1,
所以F1∈平面FCC1,
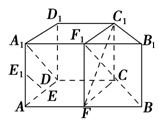
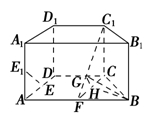
因此平面FCC1,即為平面C1CFF1.,連接A1D,F1C,由于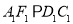
 CD,
CD,
所以四邊形A1DCF1為平行四邊形,因此A1D∥F1C.又EE1∥A1D,得EE1∥F1C.
而EE1?平面FCC1,F1C?平面FCC1,故EE1∥平面FCC1.
法二 因為F為AB的中點,CD=2,AB=4,AB∥CD,所以CD  AF.
AF.
因此四邊形AFCD為平行四邊形,所以AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC?平面FCC1,CC1?平面FCC1,
所以平面ADD1A1∥平面FCC1.又EE1?平面ADD1A1,所以EE1∥平面FCC1.
(2)解 法一 取FC的中點H,由于FC=BC=FB,所以BH⊥FC.又BH⊥CC1,CC1∩FC=C.所以BH⊥平面FCC1.過H作HG⊥C1F于G,連接BG.由于HG⊥C1F,BH⊥平面FCC1,所以C1F⊥平面BHG.因此BG⊥C1F,所以∠BGH為所求二面角的平面角.在Rt△BHG中,BH=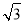 ,
,
又FH=1,且△FCC1為等腰直角三角形,所以HG=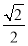 ,BG=
,BG= =
=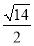 ,因此cos∠BGH=
,因此cos∠BGH=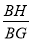 =
=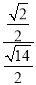 =,
=,
即所求二面角的余弦值為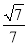 .
.
法二 過D作DR⊥CD交AB于R,以D為坐標原點建立如圖所示的空間直角坐標系,則F(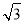 ,1,0),B(
,1,0),B(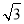 ,3,0),C(0,2,0),C1(0,2,2).
,3,0),C(0,2,0),C1(0,2,2).
所以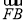 =(0,2,0),
=(0,2,0),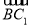 =(-
=(- ,-1,2),
,-1,2), =(
=(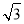 ,3,0).
,3,0).
由FB=CB=CD=DF,所以DB⊥FC.又CC1⊥平面ABCD,
所以 為平面FCC1的一個法向量.
為平面FCC1的一個法向量.
設平面BFC1的一個法向量為n=(x,y,z),
則由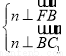 得
得 即
即 取x=1,得
取x=1,得
因此n=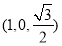 ,所以cos〈
,所以cos〈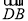 ,n〉=
,n〉= =
=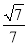 .
.
故所求二面角的余弦值為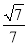 .
.


科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練3練習卷(解析版) 題型:解答題
已知函數f(x)=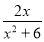 .
.
(1)若f(x)>k的解集為{x|x<-3,或x>-2},求k的值;
(2)對任意x>0,f(x)≤t恒成立,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習6-2橢圓、雙曲線、拋物線練習卷(解析版) 題型:解答題
已知橢圓C: =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ,其左、右焦點分別是F1、F2,過點F1的直線l交橢圓C于E、G兩點,且△EGF2的周長為4
,其左、右焦點分別是F1、F2,過點F1的直線l交橢圓C于E、G兩點,且△EGF2的周長為4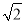 .
.
(1)求橢圓C的方程;
(2)若過點M(2,0)的直線與橢圓C相交于兩點A、B,設P為橢圓上一點,且滿足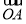 +
+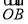 =t
=t (O為坐標原點),當|
(O為坐標原點),當|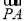 -
-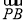 |<
|<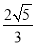 時,求實數t的取值范圍.
時,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習6-1直線與圓練習卷(解析版) 題型:選擇題
過點A(1,-1),B(-1,1),且圓心在直線x+y-2=0上的圓的方程是 ( ).
A.(x-3)2+(y+1)2=4 B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4 D.(x+1)2+(y+1)2=4
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習5-2空間向量與立體幾何練習卷(解析版) 題型:選擇題
如圖所示,正方體ABCD-A1B1C1D1的棱長為1,線段B1D1上有兩個動點E,F且EF= ,則下列結論中錯誤的是( ).
,則下列結論中錯誤的是( ).

A.AC⊥BE
B.EF∥平面ABCD
C.三棱錐A-BEF的體積為定值
D.異面直線AE,BF所成的角為定值
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習5-1空間幾何體與點等練習卷(解析版) 題型:選擇題
如圖,在正方形ABCD中,E、F分別是BC、CD的中點,AC∩EF=G.現在沿AE、EF、FA把這個正方形折成一個四面體,使B、C、D三點重合,重合后的點記為P,則在四面體P-AEF中必有( ).

A.AP⊥△PEF所在平面
B.AG⊥△PEF所在平面
C.EP⊥△AEF所在平面
D.PG⊥△AEF所在平面
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習4-2數列求和與數列的綜合應用練習卷(解析版) 題型:填空題
記[x]為不超過實數x的最大整數.例如,[2]=2,[1.5]=1,[-0.3]=-1.設a為正整數,數列{xn}滿足x1=a,xn+1= (n∈N*).現有下列命題:
(n∈N*).現有下列命題:
①當a=5時,數列{xn}的前3項依次為5,3,1;
②對數列{xn}都存在正整數k,當n≥k時總有xn=xk;
③當n≥1時,xn>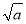 -1;
-1;
④對某個正整數k,若xk+1≥xk,則xk=[ ].
].
其中的真命題有________.(寫出所有真命題的編號)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習4-1等差數列與等比數列練習卷(解析版) 題型:選擇題
已知數列{an}為等差數列,且a1+a7+a13=4π,則tan(a2+a12)= ( ).
A.-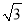 B.
B.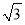
C.± D.-
D.-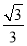
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習1-2算法與程序框圖等練習卷(解析版) 題型:解答題
某鎮政府為了更好地服務于農民,派調查組到某村考察.據了解,該村有100戶農民,且都從事蔬菜種植,平均每戶的年收入為3萬元.為了調整產業結構,該鎮政府決定動員部分農民從事蔬菜加工.據估計,若能動員x(x>0)戶農民從事蔬菜加工,則剩下的繼續從事蔬菜種植的農民平均每戶的年收入有望提高2x%,而從事蔬菜加工的農民平均每戶的年收入將為3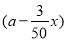 (a>0)萬元.
(a>0)萬元.
(1)在動員x戶農民從事蔬菜加工后,要使從事蔬菜種植的農民的總年收入不低于動員前從事蔬菜種植的農民的總年收入,求x的取值范圍;
(2)在(1)的條件下,要使這100戶農民中從事蔬菜加工的農民的總年收入始終不高于從事蔬菜種植的農民的總年收入,求a的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com