
小明家訂了一份報紙,寒假期間他收集了每天報紙送達時間的數據,并繪制成頻率分布直方圖,如圖所示.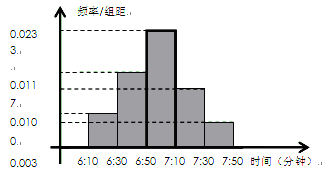
(1)根據圖中的數據信息,求出眾數 和中位數
和中位數 (精確到整數分鐘);
(精確到整數分鐘);
(2)小明的父親上班離家的時間 在上午
在上午 之間,而送報人每天在
之間,而送報人每天在 時刻前后半小時內把報紙送達(每個時間點送達的可能性相等),求小明的父親在上班離家前能收到報紙(稱為事件
時刻前后半小時內把報紙送達(每個時間點送達的可能性相等),求小明的父親在上班離家前能收到報紙(稱為事件 )的概率.
)的概率.
(1) ,
, ;(2)
;(2)
解析試題分析:(1)在頻率分步直方圖中,最高矩形的中點橫坐標代表數據的眾數;各個矩形的面積和為1,中位數是面積等分為 的軸線和橫軸的交點;平均數是各矩形的面積乘以相應矩形中點橫坐標的累加值;(2)基本事件總數有無限多個,故可以考慮幾何概型.
的軸線和橫軸的交點;平均數是各矩形的面積乘以相應矩形中點橫坐標的累加值;(2)基本事件總數有無限多個,故可以考慮幾何概型.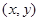 可以看成平面中的點,試驗的全部結果構成平面區域
可以看成平面中的點,試驗的全部結果構成平面區域 ,而事件A發生的前提是
,而事件A發生的前提是 ,利用面積的比表示事件A發生的概率
,利用面積的比表示事件A發生的概率 .
.
試題解析:(1) 2分
2分
由頻率分布直方圖可知 即
即 , 3分
, 3分
∴

解得 分即
分即 6分
6分
(2)設報紙送達時間為 7分
7分
則小明父親上班前能取到報紙等價于 , 10分
, 10分
如圖可知,所求概率為 13分
13分
考點:1、頻率分布直方圖;2、眾數和中位數;3、幾何概型.


科目:高中數學 來源: 題型:解答題
下表是某市從3月份中隨機抽取的 天空氣質量指數(
天空氣質量指數( )和“
)和“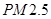 ”(直徑小于等于
”(直徑小于等于 微米的顆粒物)
微米的顆粒物) 小時平均濃度的數據,空氣質量指數(
小時平均濃度的數據,空氣質量指數( )小于
)小于 表示空氣質量優良.
表示空氣質量優良.
| 日期編號 |  |  |  |  |  |  |  |  |  |  |
空氣質量指數( ) ) |  |  |  |  |  |  |  |  |  |  |
“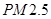 ” ” 小時平均濃度( 小時平均濃度(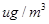 ) ) |  |  |  |  |  |  |  |  |  |  |
 為“抽取的兩個日期中,當天‘
為“抽取的兩個日期中,當天‘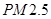 ’的
’的 小時平均濃度不超過
小時平均濃度不超過 ”,求事件
”,求事件 發生的概率.
發生的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商店試銷某種商品20天,獲得如下數據:
| 日銷售量(件) | 0 | 1 | 2 | 3 |
| 頻數 | 1 | 5 | 9 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 .
.
(1)從區間 內任取一個實數
內任取一個實數 ,設事件
,設事件 ={函數
={函數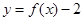 在區間
在區間 上有兩個不同的零點},求事件
上有兩個不同的零點},求事件 發生的概率;
發生的概率;
(2)若連續擲兩次骰子(骰子六個面上標注的點數分別為 )得到的點數分別為
)得到的點數分別為 和
和 ,記事件
,記事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩射手在同一條件下進行射擊,分布列如下:射手甲擊中環數8,9,10的概率分別為0.2,0.6,0.2;射手乙擊中環數8,9,10的概率分別為0.4,0.2,0.4.用擊中環數的期望與方差比較兩名射手的射擊水平.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有一種闖三關游戲規則規定如下:用拋擲正四面體型骰子(各面上分別有1,2,3,4點數的質地均勻的正四面體)決定是否過關,在闖第n(n=1,2,3)關時,需要拋擲n次骰子,當n次骰子面朝下的點數之和大于n2時,則算闖此關成功,并且繼續闖關,否則停止闖關.每次拋擲骰子相互獨立.
(1)求僅闖過第一關的概率;
(2)記成功闖過的關數為ξ,求ξ的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學為豐富教工生活,國慶節舉辦教工趣味投籃比賽,有 、
、 兩個定點投籃位置,在
兩個定點投籃位置,在 點投中一球得2分,在
點投中一球得2分,在 點投中一球得3分.其規則是:按先
點投中一球得3分.其規則是:按先 后
后 再
再 的順序投
的順序投
籃.教師甲在 和
和 點投中的概率分別是
點投中的概率分別是 ,且在
,且在 、
、 兩點投中與否相互獨立.
兩點投中與否相互獨立.
(1)若教師甲投籃三次,試求他投籃得分X的分布列和數學期望;
(2)若教師乙與甲在A、B點投中的概率相同,兩人按規則各投三次,求甲勝乙的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com