(本小題滿分14分)已知四棱錐P—ABCD的三視圖如右圖所示,
其中正(主)視圖與側(左)視為直角三角形,俯視圖為正方形。

(1)求四棱錐P—ABCD的體積;

(2)若E是側棱

上的動點。問:不論點E在PA的
任何位置上,是否都有

?
請證明你的結論?
(3)求二面角D—PA—B的余弦值。
解:(1)由三視圖可知,四棱錐P—ABCD的底面是邊長為1的正方形,
側棱
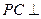
底面ABCD,且PC=2
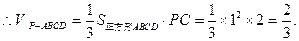
4分
(2)不論點E在何位置,都有
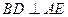
5分
證明:連結AC,
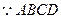
是正方形,
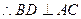
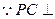
底面ABCD,且
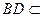
平面ABCD,
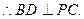
6分
又
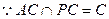
,
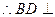
平面PAC 7分
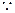
不論點E在何位置,都有
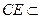
平面PAC。
不論點E在何位置,都有BD

CE。 9分
(3)在平面DAP過點D作DF

PA于F,連結BF

,AD=AB=1,
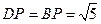
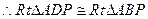
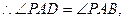
又AF=AF,AB=AD
從而
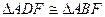
,
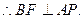
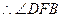
為二面角D—AP—B的平面角 12分
在
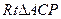
中,
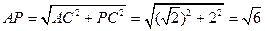
故在
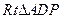
中,

又
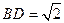
,在
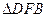
中,
由余弦定理得:
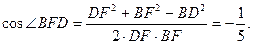
所以二面角D—PA—B的余弦值為
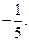
14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
:一個長方體去掉一個小長方體,所得幾何體的正(主)視圖與側(左)視圖分別如右圖所示,則該幾何體的俯視圖為
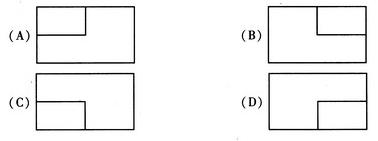
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若一個正三棱柱的三視圖如下圖所示,則這個正三棱柱的高和底面邊長分別為( )
A.2,2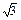 | B.2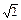 ,2 ,2 | C.4,2 | D.2,4 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下列幾何體中,正視圖、側視圖、俯視圖都相同的幾何體的序號是( )
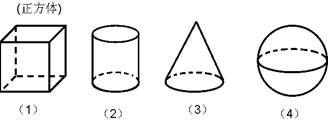
| A.(1)(2) | B.(2)(3) | C.(3)(4) | D.(1)(4) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
有一個幾何體是由幾個相同的正方體拼合而成(如圖2),則這個幾何體含有的正方體的個數(shù)是
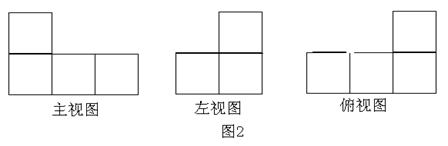
| A.7 | B.6 | C.5 | D.4 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在正方體
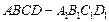
中,
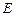
,
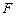
分別為
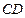
和

的中點,則直線
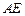
與
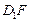
所成角的余弦值為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設A,B兩地位于北緯

的緯線上,且兩地的經(jīng)度差為

,若地球的半徑為
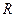
千米,且時速為20千米的輪船從A地到B地最少需要
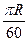
小時,則
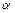
為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,在三棱錐
P—ABC中,
AB⊥
 BC
BC,
AB =" BC" = kPA,點
E、D分別是
AC、PC的中點,
EP⊥底面
ABC.

(1) 求證:
ED∥平面
PAB;
(2) 求

直線
AB與平面
PAC所成的角;
(3) 當
k取何值時,
E在平面
PBC內的射影恰好為△
PBC的重心?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分13分)
平面
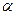
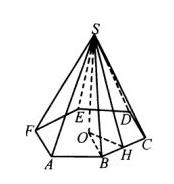
內有一個正六邊形ABCDEF,它的中心是O,邊長是2cm.OS⊥
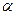
,OS=4cm.
求:點S到這個正六邊形頂

點和邊的距離.
查看答案和解析>>

 (1)求四棱錐P—ABCD的體積;
(1)求四棱錐P—ABCD的體積; (2)若E是側棱
(2)若E是側棱 上的動點。問:不論點E在PA的
上的動點。問:不論點E在PA的 ?
?
 的緯線上,且兩地的經(jīng)度差為
的緯線上,且兩地的經(jīng)度差為 ,若地球的半徑為
,若地球的半徑為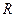 千米,且時速為20千米的輪船從A地到B地最少需要
千米,且時速為20千米的輪船從A地到B地最少需要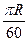 小時,則
小時,則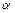 為
為 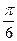
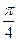
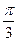
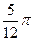
 BC,AB =" BC" = kPA,點E、D分別是AC、PC的中點,EP⊥底面ABC.
BC,AB =" BC" = kPA,點E、D分別是AC、PC的中點,EP⊥底面ABC.
 直線AB與平面PAC所成的角;
直線AB與平面PAC所成的角;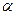 內有一個正六邊形ABCDEF,它的中心是O,邊長是2cm.OS⊥
內有一個正六邊形ABCDEF,它的中心是O,邊長是2cm.OS⊥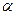 ,OS=4cm.
,OS=4cm. 點和邊的距離.
點和邊的距離.