
【題目】已知![]() 為雙曲線
為雙曲線![]() 的左右焦點,M為雙曲線左支上的點,
的左右焦點,M為雙曲線左支上的點,![]() 的周長是18,動點P在雙曲線的右支上,則
的周長是18,動點P在雙曲線的右支上,則![]() 面積的取值范圍是( )
面積的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
求出雙曲線的![]() 的值及
的值及![]() ,
,![]() ,設
,設![]() ,
,![]() ,可求出
,可求出![]() ,可得
,可得![]() ,直線
,直線![]() 的斜率與漸近線斜率相等,設
的斜率與漸近線斜率相等,設![]() ,可得當
,可得當![]() 且P點位于第一象限內
且P點位于第一象限內![]() 面積最小,
面積最小,![]() 且P點位于第四象限內,
且P點位于第四象限內,![]() 的面積最大,計算可得答案.
的面積最大,計算可得答案.
解:由![]() 為雙曲線
為雙曲線![]() 的左右焦點,可得
的左右焦點,可得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,由
,由![]() 的周長是18,
的周長是18,
可得![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
設![]() ,且
,且![]() ,由點
,由點![]() 在曲線上,且
在曲線上,且![]() ,
,
可得:![]() 且
且![]() ,可得
,可得![]() ,
,
可得: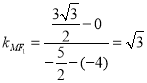 ,可得漸近線方程為:
,可得漸近線方程為:![]() ,
,
可得直線![]() 的斜率與漸近線斜率相等,故在右支上不存在斜率與
的斜率與漸近線斜率相等,故在右支上不存在斜率與![]() 相等且與右支相切的直線,設
相等且與右支相切的直線,設![]()
則![]() 面積最小時為
面積最小時為![]() 且P點位于第一象限內,此時點P到線段
且P點位于第一象限內,此時點P到線段![]() 的距離等價于漸進線
的距離等價于漸進線![]() 到直線
到直線![]() 的距離,
的距離,
易得![]() 的直線方程為:
的直線方程為:![]() ,可得漸近線
,可得漸近線![]() 上
上![]() 到直線
到直線![]() 的距離:
的距離:![]() ,可得
,可得![]() 的最小值為:
的最小值為:![]() ,
,
當![]() 且P點位于第四象限內,
且P點位于第四象限內,![]() 的面積最大為
的面積最大為![]() ,
,
故可得:![]() 面積的取值范圍是
面積的取值范圍是![]() ,
,
故選:A.


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】某調研機構,對本地![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有
人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有![]() 人為“低碳族”,該
人為“低碳族”,該![]() 人的年齡情況對應的頻率分布直方圖如圖.
人的年齡情況對應的頻率分布直方圖如圖.

(1)根據頻率分布直方圖,估計這![]() 名“低碳族”年齡的平均值,中位數;
名“低碳族”年齡的平均值,中位數;
(2)若在“低碳族”且年齡在![]() 、
、![]() 的兩組人群中,用分層抽樣的方法抽取
的兩組人群中,用分層抽樣的方法抽取![]() 人,試估算每個年齡段應各抽取多少人?
人,試估算每個年齡段應各抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣mx2,g(x)=![]() +x,m∈R,令F(x)=f(x)+g(x).
+x,m∈R,令F(x)=f(x)+g(x).
(Ⅰ)當m=![]() 時,求函數f(x)的單調遞增區間;
時,求函數f(x)的單調遞增區間;
(Ⅱ)若關于x的不等式F(x)≤mx﹣1恒成立,求整數m的最小值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在
在![]() 處的切線
處的切線![]() 與直線
與直線![]() 平行.
平行.
(1)求實數![]() 的值;
的值;
(2)若函數![]() 在
在![]() 上恰有兩個零點,求實數
上恰有兩個零點,求實數![]() 的取值范圍.
的取值范圍.
(3)記函數![]() ,設
,設![]() 是函數
是函數![]() 的兩個極值點,若
的兩個極值點,若![]() ,且
,且![]() 恒成立,求實數
恒成立,求實數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題:①命題“若![]() ,則
,則![]() ”的逆否命題為“若
”的逆否命題為“若![]() ,則
,則![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的充分不必要條件; ③若
”的充分不必要條件; ③若![]() 為假命題,則
為假命題,則![]() 均為假命題;④對于命題
均為假命題;④對于命題![]() 使得
使得![]() ,則
,則![]() 為
為![]() ,均有
,均有![]() .其中,真命題的個數是 ( )
.其中,真命題的個數是 ( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為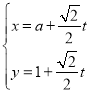 (
(![]() 為參數,
為參數,![]() ).以
).以![]() 為極點,
為極點,![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知曲線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面ABC.
平面ABC.
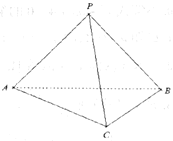
(1)求證:![]() 平面PBC;
平面PBC;
(2)求二面角P-AC-B的余弦值;
(3)求直線BC與平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某周末,鄭州方特夢幻王國匯聚了八方來客.面對該園區內相鄰的兩個主題公園“千古蝶戀”和“西游傳說”,成年人和未成年人選擇游玩的意向會有所不同.某統計機構對園區內的100位游客(這些游客只在兩個主題公園中二選一)進行了問卷調查.調查結果顯示,在被調查的50位成年人中,只有10人選擇“西游傳說”,而選擇“西游傳說”的未成年人有20人.
(1)根據題意,請將下面的![]() 列聯表填寫完整;
列聯表填寫完整;
選擇“西游傳說” | 選擇“千古蝶戀” | 總計 | |
成年人 | |||
未成年人 | |||
總計 |
(2)根據列聯表的數據,判斷是否有![]() 的把握認為選擇哪個主題公園與年齡有關.
的把握認為選擇哪個主題公園與年齡有關.
附參考公式與表: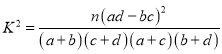 (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com