
【題目】等差數(shù)列{an}的前n項和記為Sn , 已知a10=30,a20=50.
(1)求通項{an};
(2)令Sn=242,求n.
科目:高中數(shù)學 來源: 題型:
【題目】橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,過右焦點
,過右焦點![]() 垂直于
垂直于![]() 軸的直線與橢圓交于
軸的直線與橢圓交于![]() ,
, ![]() 兩點且
兩點且![]() ,又過左焦點
,又過左焦點![]() 任作直線
任作直線![]() 交橢圓于點
交橢圓于點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)橢圓![]() 上兩點
上兩點![]() ,
, ![]() 關于直線
關于直線![]() 對稱,求
對稱,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定義A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某租賃公司擁有汽車100輛.當每輛車的月租金為3000元時,可全部租出,當每輛車的月租金每增加50元時,未租出的車將會增加一輛,租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.,當每輛車的月租金定為x元時,租賃公司的月收益為y元,
(1)試寫出x,y的函數(shù)關系式(不要求寫出定義域);
(2)租賃公司某月租出了88輛車,求租賃公司的月收益多少元?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知等差數(shù)列{an}滿足an+1>an , a1=1,且該數(shù)列的前三項分別加上1,1,3后順次成為等比數(shù)列{bn}的前三項.
(1)求數(shù)列{an},{bn}的通項公式;
(2)令cn=anbn , 求數(shù)列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
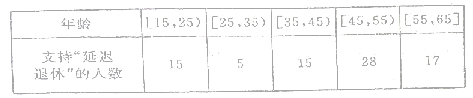
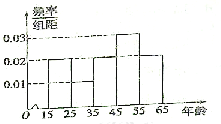
【題目】中央政府為了應對因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”,為了了解人們對“延遲退休年齡政策”的態(tài)度,責成人社部進行調(diào)研,人社部從網(wǎng)上年齡在![]() 歲的人群中隨機調(diào)查100人,調(diào)查數(shù)據(jù)的頻率分布直方圖和支持“延遲退休”的人數(shù)與年齡的統(tǒng)計結果如下:
歲的人群中隨機調(diào)查100人,調(diào)查數(shù)據(jù)的頻率分布直方圖和支持“延遲退休”的人數(shù)與年齡的統(tǒng)計結果如下:
(1)由以上統(tǒng)計數(shù)據(jù)填![]() 列聯(lián)表,并判斷是否95%的把握認為以
列聯(lián)表,并判斷是否95%的把握認為以![]() 歲為界點的不同人群對“延遲退休年齡政策”的支持有差異;
歲為界點的不同人群對“延遲退休年齡政策”的支持有差異;

(2)若以![]() 歲為分界點,從不支持“延遲退休”的人中按分層抽樣的方法抽取
歲為分界點,從不支持“延遲退休”的人中按分層抽樣的方法抽取![]() 人參加某項活動,現(xiàn)從這
人參加某項活動,現(xiàn)從這![]() 人中隨機抽
人中隨機抽![]() 人.
人.
①抽到![]() 人是
人是![]() 歲以下時,求抽到的另一人是
歲以下時,求抽到的另一人是![]() 歲以上的概率;
歲以上的概率;
②記抽到![]() 歲以上的人數(shù)為
歲以上的人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
|
|
|
|
|
|
|
|
|
|
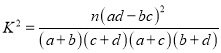
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,已知點
中,已知點![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).以原點為極點,
為參數(shù)).以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為 .
.
(Ⅰ)判斷點![]() 與直線
與直線![]() 的位置關系并說明理由;
的位置關系并說明理由;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 的兩個交點分別為
的兩個交點分別為![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列四組函數(shù)中,是同一個函數(shù)的是( )
A.![]() ,
, ![]()
B.f(x)=2log2x, ![]()
C.f(x)=ln(x﹣1)﹣ln(x+1), ![]()
D.f(x)=lg(1﹣x)+lg(1+x),g(x)=lg(1﹣x2)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com