
【題目】已知函數![]() 存在唯一極值點。
存在唯一極值點。
(I)求![]() 的取值范圍;
的取值范圍;
(II)證明:函數![]() 與
與![]() 的值域相同。
的值域相同。
【答案】(I)![]() ;(II)詳見解析.
;(II)詳見解析.
【解析】試題分析:
(Ⅰ)由題意可得: ![]() ,
, ![]() ,
,
分類討論:當![]() 時,
時, ![]() 在
在![]() 內有唯一極值點;
內有唯一極值點;
當![]() 時,若
時,若![]() ,
, ![]() 無極值點,若
無極值點,若![]() ,
, ![]() 有兩個極值點,不合題意;則
有兩個極值點,不合題意;則![]() ;
;
(Ⅱ)由(Ⅰ)知, ![]() ,設
,設![]() ,則
,則![]() 在
在![]() 上單減,在
上單減,在![]() 上單增,
上單增, ![]() 的值域為
的值域為![]() ,則原問題等價于
,則原問題等價于![]() ,即
,即![]() ,整理變形為
,整理變形為![]() ,導函數
,導函數![]() 單增,則原問題等價于
單增,則原問題等價于![]() ,據此命題得證.
,據此命題得證.
試題解析:
(Ⅰ)![]() ,
, ![]() ,當
,當![]() 時,
時, ![]() ,
,
故![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() 時,
時, ![]() ,
, ![]() ,
,
故![]() 在
在![]() 內有唯一實根,即
內有唯一實根,即![]() 在
在![]() 內有唯一極值點;
內有唯一極值點;
當![]() 時,由
時,由![]() 得
得![]() ,故
,故![]() 在
在![]() 上單增,在
上單增,在![]() 上單減,
上單減,
若![]() 則
則![]() 恒成立,此時
恒成立,此時![]() 無極值點,若
無極值點,若![]() ,
,
又![]() 時
時![]() ,
, ![]() 時
時![]() ,此時
,此時![]() 有兩個極值點;
有兩個極值點;
綜上, ![]() ;
;
(Ⅱ)由(Ⅰ)知, ![]() ,設
,設![]() 即
即![]() ,
,
則![]() 在
在![]() 上單減,在
上單減,在![]() 上單增,
上單增, ![]() 的值域為
的值域為![]() ,
,
要使![]() 與
與![]() 的值域相同,只需
的值域相同,只需![]() ,即
,即![]() ,
,
即![]() ,又
,又![]() ,故
,故![]() 即
即![]() ,
,
故只需證![]() ,又
,又![]() 單增,所以要證
單增,所以要證![]() 即證
即證![]() ,
,
而![]() ,故得證.
,故得證.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:
【題目】某市準備引進優秀企業進行城市建設. 城市的甲地、乙地分別對5個企業(共10個企業)進行綜合評估,得分情況如莖葉圖所示.

(Ⅰ)根據莖葉圖,求乙地對企業評估得分的平均值和方差;
(Ⅱ)規定得分在85分以上為優秀企業. 若從甲、乙兩地準備引進的優秀企業中各隨機選取1個,求這兩個企業得分的差的絕對值不超過5分的概率.
注:方差![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查銀川市某校高中生是否愿意提供志愿者服務,用簡單隨機抽樣方法從該校調查了50人,結果如下:

(1)用分層抽樣的方法在愿意提供志愿者服務的學生中抽取6人,其中男生抽取多少人?
(2)在(1)中抽取的6人中任選2人,求恰有一名女生的概率;
(3)你能否在犯錯誤的概率不超過0.010的前提下,認為該校高中生是否愿意提供志愿者服務與性別有關?
下面的臨界值表供參考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
獨立性檢驗統計量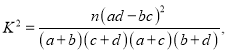 其中
其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠為預測產品的回收率![]() ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量![]() 之間的相關關系,現收集了4組對照數據。
之間的相關關系,現收集了4組對照數據。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)請根據相關系數![]() 的大小判斷回收率
的大小判斷回收率![]() 與
與![]() 之間是否存在高度線性相關關系;
之間是否存在高度線性相關關系;
(Ⅱ)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測當
,并預測當![]() 時回收率
時回收率![]() 的值.
的值.
參考數據: 
| 1 | 0 |
|
| 其他 |
| 完全相關 | 不相關 | 高度相關 | 低度相關 | 中度相關 |
 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,
, ![]() 上的動點
上的動點![]() 到兩焦點的距離之和為4,當點
到兩焦點的距離之和為4,當點![]() 運動到橢圓
運動到橢圓![]() 的上頂點時,直線
的上頂點時,直線![]() 恰與以原點
恰與以原點![]() 為圓心,以橢圓
為圓心,以橢圓![]() 的離心率為半徑的圓相切.
的離心率為半徑的圓相切.
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() 的左右頂點分別為
的左右頂點分別為![]() ,若
,若![]() 交直線
交直線![]() 于
于![]() 兩點.問以
兩點.問以![]() 為直徑的圓是否過定點?若過定點,請求出該定點坐標;若不過定點,請說明理由.
為直徑的圓是否過定點?若過定點,請求出該定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的是__________(填序號)
①命題“![]() ,有
,有![]() ”的否定是“
”的否定是“![]() ”,有
”,有![]() ”;
”;
②已知![]() ,
, ![]() ,
, ![]() ,則
,則![]() 的最小值為
的最小值為![]() ;
;
③設![]() ,命題“若
,命題“若![]() ,則
,則![]() ”的否命題是真命題;
”的否命題是真命題;
④已知![]() ,
, ![]() ,若命題
,若命題![]() 為真命題,則
為真命題,則![]() 的取值范圍是
的取值范圍是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若由方程x2-y2=0和x2+(y-b)2=2所組成的方程組至多有兩組不同的實數解,則實數b的取值范圍是( )
A. b≥2![]() 或b≤-2
或b≤-2![]() B. b≥2或b≤-2
B. b≥2或b≤-2
C. -2≤b≤2 D. -2![]() ≤b≤2
≤b≤2![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率都為![]() ,現采用隨機模擬的方法估計該運動員三次投籃都命中的概率:先由計算機產生0到9之間取整數值的隨機數,指定1,2,3,4,5表示命中;6,7,8,9,0表示不命中,再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
,現采用隨機模擬的方法估計該運動員三次投籃都命中的概率:先由計算機產生0到9之間取整數值的隨機數,指定1,2,3,4,5表示命中;6,7,8,9,0表示不命中,再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
162 966 151 525 271 932 592 408 569 683
471 257 333 027 554 488 730 163 537 989
據此估計,該運動員三次投籃都命中的概率為
A. 0.15 B. 0.2 C. 0.25 D. 0.35
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com