
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0),四點P1(1,1),P2(0,1),P3(﹣1,
=1(a>b>0),四點P1(1,1),P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.(12分)
)中恰有三點在橢圓C上.(12分)
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為﹣1,證明:l過定點.
【答案】
(1)
解:根據橢圓的對稱性,P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )兩點必在橢圓C上,
)兩點必在橢圓C上,
又P4的橫坐標為1,∴橢圓必不過P1(1,1),
∴P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )三點在橢圓C上.
)三點在橢圓C上.
把P2(0,1),P3(﹣1, ![]() )代入橢圓C,得:
)代入橢圓C,得:
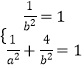 ,解得a2=4,b2=1,
,解得a2=4,b2=1,
∴橢圓C的方程為 ![]() =1.
=1.
(2)
證明:①當斜率不存在時,設l:x=m,A(m,yA),B(m,﹣yA),
∵直線P2A與直線P2B的斜率的和為﹣1,
∴ ![]() =
= ![]() =
= ![]() =﹣1,
=﹣1,
解得m=2,此時l過橢圓右頂點,不存在兩個交點,故不滿足.
②當斜率存在時,設l:y=kx+b,(b≠1),A(x1,y1),B(x2,y2),
聯立 ![]() ,整理,得(1+4k2)x2+8kbx+4b2﹣4=0,
,整理,得(1+4k2)x2+8kbx+4b2﹣4=0,
![]() ,x1x2=
,x1x2= ![]() ,
,
則 ![]() =
= ![]() =
= ![]()
=  =
= ![]() =﹣1,又b≠1,
=﹣1,又b≠1,
∴b=﹣2k﹣1,此時△=﹣64k,存在k,使得△>0成立,
∴直線l的方程為y=kx﹣2k﹣1,
當x=2時,y=﹣1,
∴l過定點(2,﹣1).
【解析】(1.)根據橢圓的對稱性,得到P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )三點在橢圓C上.把P2(0,1),P3(﹣1,
)三點在橢圓C上.把P2(0,1),P3(﹣1, ![]() )代入橢圓C,求出a2=4,b2=1,由此能求出橢圓C的方程.
)代入橢圓C,求出a2=4,b2=1,由此能求出橢圓C的方程.
(2.)當斜率不存在時,不滿足;當斜率存在時,設l:y=kx+b,(b≠1),聯立 ![]() ,得(1+4k2)x2+8kbx+4b2﹣4=0,由此利用根的判別式、韋達定理、直線方程,結合已知條件能證明直線l過定點(2,﹣1).
,得(1+4k2)x2+8kbx+4b2﹣4=0,由此利用根的判別式、韋達定理、直線方程,結合已知條件能證明直線l過定點(2,﹣1).
【考點精析】本題主要考查了斜截式方程和橢圓的標準方程的相關知識點,需要掌握直線的斜截式方程:已知直線![]() 的斜率為
的斜率為![]() ,且與
,且與![]() 軸的交點為
軸的交點為![]() 則:
則:![]() ;橢圓標準方程焦點在x軸:
;橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能正確解答此題.
才能正確解答此題.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E為PB上的點,且2BE=EP. 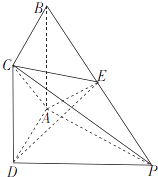
(1)證明:AC⊥DE;
(2)若PC= ![]() BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于![]() 與
與![]() 有表格中的數據,且
有表格中的數據,且![]() 與
與![]() 線性相關,由最小二乘法得
線性相關,由最小二乘法得![]() .
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求![]() 與
與![]() 的線性回歸方程;
的線性回歸方程;
(2)現有第二個線性模型:![]() ,且
,且![]() .若與(1)的線性模型比較,哪一個線性模型擬合效果比較好,請說明理由
.若與(1)的線性模型比較,哪一個線性模型擬合效果比較好,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中:
①若![]() ,滿足
,滿足![]() ,則
,則![]() 的最大值為
的最大值為![]() ;
;
②若![]() ,則函數
,則函數![]() 的最小值為
的最小值為![]()
③若![]() ,滿足
,滿足![]() ,則
,則![]() 的最小值為
的最小值為![]()
④函數![]() 的最小值為
的最小值為![]()
正確的有__________.(把你認為正確的序號全部寫上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 兩地相距
兩地相距![]() 千米,汽車從
千米,汽車從![]() 地勻速行駛到
地勻速行駛到![]() 地,速度不超過
地,速度不超過![]() 千米小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分兩部分組成:可變部分與速度
千米小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分兩部分組成:可變部分與速度![]() 的平方成正比,比例系數為
的平方成正比,比例系數為![]() ,固定部分為
,固定部分為![]() 元,
元,
(1)把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() (千米小時)的函效:并求出當
(千米小時)的函效:并求出當![]() 時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
(2)隨著汽車的折舊,運輸成本會發生一些變化,那么當![]() ,此時汽車的速度應調整為多大,才會使得運輸成本最小,
,此時汽車的速度應調整為多大,才會使得運輸成本最小,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{xn}是各項均為正數的等比數列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求數列{xn}的通項公式;
(Ⅱ)如圖,在平面直角坐標系xOy中,依次連接點P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折線P1 P2…Pn+1 , 求由該折線與直線y=0,x=x1 , x=xn+1所圍成的區域的面積Tn . 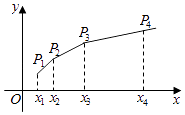
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學名著《九章算術》中“竹九節”問題曰:“今有竹九節,下三節容量四升,上四節容量三升,問中間兩節欲均容各多少?”其意為:“現有一根9節的竹子,自上而下的容積成等差數列,下面3節容量為4升,上面4節容積為3升,問中間2節各多少容積?”則中間2節容積合計________升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知△ABC的面積為 ![]() .(12分)
.(12分)
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com