Question

【題目】如圖，是以為直徑的半圓上異于點的點，矩形所在的平面垂直于該半圓所在平面，且

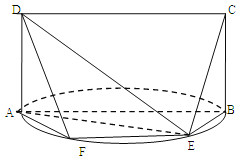
(Ⅰ)求證：；

(Ⅱ)設平面與半圓弧的另一個交點為,

①求證：//;

②若，求三棱錐E-ADF的體積．

Answer 1

【答案】(1)通過證明面，進而得到線線垂直的證明。

(2)利用平面的性質(zhì)定理，可知線線平行，體積為

【解析】

試題（1）證明線線垂直，則可轉化為線面垂直，由于圓周角的定義，則知，由矩形所在的平面垂直于該半圓所在平面，及面面垂直性質(zhì)定理得面，則可得平面平面

根據(jù)垂直的有關性質(zhì)定理，則可得平面，故

（2）①證明線線平行，則可用過平面的一個平行線作于該平面相交的平面，則該直線與交線平行由,得平面，又由平面平面于直線，則根據(jù)線面平行的性質(zhì)定理得,由平行的傳遞性得；②則體積可以用多種方法，有直接求法、割補法、轉化法，對于此題可轉化后用直接求法，求三棱錐E-ADF先轉化;根據(jù)三棱錐的體積公式，則有

試題解析：

是半圓上異于的點， ，又矩形所在的平面垂直于該半圓所在平面由面面垂直性質(zhì)定理得面，平面平面 平面,故．

（2）① 由,得平面,又平面平面于直線，根據(jù)線面平行的性質(zhì)定理得,故,②．