
【題目】已知橢圓C: ![]() (a>b>0),長軸長為4,離心率為
(a>b>0),長軸長為4,離心率為![]() .
.
(Ⅰ)橢圓的求橢圓的標準方程;
(Ⅱ)設過定點M(0,2)的直線l與橢圓C交于不同的兩點A,B,且∠AOB為銳角(O為坐標原點),求直線l的斜率k的取值范圍.
【答案】(Ⅰ) ![]() +y2=1(Ⅱ)k∈(-2,-
+y2=1(Ⅱ)k∈(-2,- ![]() )∪(
)∪(![]() ,2).
,2).
【解析】試題分析:(1)由題意可得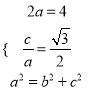 ,解得即可;
,解得即可;
(2)直線![]() 的方程為
的方程為![]() ,設
,設![]() .與橢圓方程聯立,由
.與橢圓方程聯立,由![]() ,解得
,解得![]() 的取值范圍.可得根與系數的關系.若
的取值范圍.可得根與系數的關系.若![]() 為銳角,則
為銳角,則![]() ,把根與系數的關系代入又得到
,把根與系數的關系代入又得到![]() 的取值范圍,取其交集即可.
的取值范圍,取其交集即可.
試題解析:(Ⅰ)依題意, 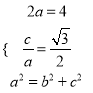 ,解得
,解得![]() ,
,
故橢圓C的方程為![]() +y2=1.
+y2=1.
(Ⅱ)如圖,依題意,直線l的斜率必存在,
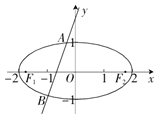
設直線l的方程為y=kx+2,A(x1,y1),B(x2,y2),
聯立方程組 ,消去y整理得(1+4k2)x2+16kx+12=0,
,消去y整理得(1+4k2)x2+16kx+12=0,
由韋達定理,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=![]() +
+![]() +4=
+4=![]() ,
,
因為直線l與橢圓C相交,則Δ>0,
即256k2-48(1+4k2)>0,
解得k<-![]() 或k>
或k>![]() ,
,
當∠AOB為銳角時,向量![]() ,則x1x2+y1y2>0,
,則x1x2+y1y2>0,
即![]() +
+![]() >0,解得-2<k<2,
>0,解得-2<k<2,
故當∠AOB為銳角時,k∈(-2,- ![]() )∪(
)∪(![]() ,2).
,2).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知a,b分別是△ABC內角A,B的對邊,且bsin2A=![]() acos Asin B,函數f(x)=sin Acos2x-sin2
acos Asin B,函數f(x)=sin Acos2x-sin2![]() sin 2x,x∈
sin 2x,x∈![]() .
.
(1)求A;
(2)求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐PABC中,不能證明AP⊥BC的條件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設向量![]() ,
, ![]() ,記
,記![]()
(1)求函數f(x)的最小正周期;
(2)試用“五點法”畫出函數f(x)在區間![]() 上的簡圖,并指出該函數的圖象可由y=sin x(x∈R)的圖象經過怎樣的平移和伸縮變換得到;
上的簡圖,并指出該函數的圖象可由y=sin x(x∈R)的圖象經過怎樣的平移和伸縮變換得到;
(3)若函數g(x)=f(x)+m, ![]() 的最小值為2,試求出函數g(x)的最大值.
的最小值為2,試求出函數g(x)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高三文科班學生參加了數學與地理水平測試,學校從測試合格的學生中隨機抽取100人的成績進行統計分析.抽取的100人的數學與地理的水平測試成績如下表:

成績分為優秀、良好、及格三個等級,橫向、縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有20+18+4=42人.
(1)若在該樣本中,數學成績優秀率為30%,求a,b的值;
(2)若樣本中![]() ,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
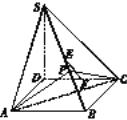
【題目】四棱錐S-ABCD中的底面是菱形,∠BAD=60°,SD⊥底面ABCD,SD=AB=2,E、F分別為SB、CD的中點.
(Ⅰ)求證:EF∥平面SAD;
(Ⅱ)點P是SB上一點,若SB⊥平面APC,試確定點P的位置.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com