
在△ABC中,角A,B,C所對邊分別為a,b,c,且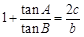 .
.
(Ⅰ)求角A;
(Ⅱ)若m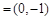 ,n
,n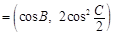 ,試求|m
,試求|m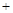 n|的最小值.
n|的最小值.
(I)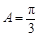 .(II)
.(II)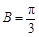 時,|m
時,|m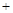 n|
n| 取得最小值
取得最小值 .
.
解析試題分析:(1)切化為弦的思想,結合兩角和差的公式得到求解的角A的值。
(2)在已知中根據向量的平方等于向量的模的平方得到關于角B,C是關系式,然后結合三角函數的性質得到最值
解:(I)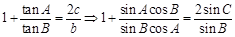 ,
,
即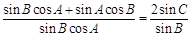 ,∴
,∴ ,∴
,∴ .
.
∵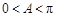 ,∴
,∴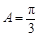 .…………………………………………………(6分)
.…………………………………………………(6分)
(II)m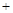 n
n 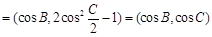 ,
,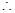 |m
|m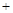 n|
n| .
.
∵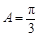 ,∴
,∴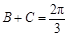 ,∴
,∴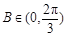 ,且
,且 .從而
.從而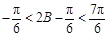 .
.
∴當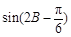 =1,即
=1,即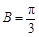 時,|m
時,|m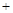 n|
n| 取得最小值
取得最小值 .………………(12分)
.………………(12分)
考點:本題主要考查同角關系的運用,以及兩角和差關系的綜合運用問題。
點評:解決該試題的關鍵是借助于向量的關系式得到三角關系式,化簡為單一函數,借助于三角函數的性質得到函數的值域。


科目:高中數學 來源: 題型:解答題
(本題滿分14分) 本題共有2個小題,第1小題滿分6分,第2小題滿分8分.
(文)某種型號汽車的四個輪胎半徑相同,均為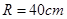 ,該車的底盤與輪胎中心在同一水平面上. 該車的涉水安全要求是:水面不能超過它的底盤高度. 如圖所示:某處有一“坑形”地面,其中坑
,該車的底盤與輪胎中心在同一水平面上. 該車的涉水安全要求是:水面不能超過它的底盤高度. 如圖所示:某處有一“坑形”地面,其中坑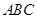 形成頂角為
形成頂角為 的等腰三角形,且
的等腰三角形,且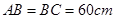 ,如果地面上有
,如果地面上有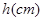 (
( )高的積水(此時坑內全是水,其它因素忽略不計).
)高的積水(此時坑內全是水,其它因素忽略不計).
(1)當輪胎與 、
、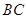 同時接觸時,求證:此輪胎露在水面外的高度(從輪胎最上部到水面的距離)為
同時接觸時,求證:此輪胎露在水面外的高度(從輪胎最上部到水面的距離)為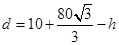 ;
;
(2) 假定該汽車能順利通過這個坑(指汽車在過此坑時,符合涉水安全要求),求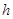 的最大值.
的最大值.
(精確到1cm).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com