Question

【題目】設函數，曲線在點處的切線方程為.

（1）求的解析式；

（2）證明：曲線上任一點處的切線與直線和直線所圍成的三角形面積為定值，并求此定值.

Answer 1

【答案】(1) ；(2)證明見解析.

【解析】解：(1)方程7x－4y－12＝0可化為y＝x－3，

當x＝2時，y＝．

又f′(x)＝a＋，

于是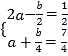，解得

故f(x)＝x－．

(2)證明：設P(x0，y0)為曲線上任一點，由f′(x)＝1＋知，曲線在點P(x0，y0)處的切線方程為y－y0＝(1＋)·(x－x0)，即y－(x0－)＝(1＋)(x－x0)．

令x＝0得，y＝－，從而得切線與直線x＝0，交點坐標為(0，－ )．

令y＝x，得y＝x＝2x0，從而得切線與直線y＝x的交點坐標為(2x0,2x0)．

所以點P(x0，y0)處的切線與直線x＝0，y＝x所圍成的三角形面積為|－||2x0|＝6．

曲線y＝f(x)上任一點處的切線與直線x＝0和直線y＝x所圍成的三角形面積為定值，此定值為6．