【題目】某港口某天0時至24時的水深
（米）隨時間
（時）變化曲線近似滿足如下函數模型
（
）.若該港口在該天0時至24時內，有且只有3個時刻水深為3米，則該港口該天水最深的時刻不可能為（ ）
A.16時B.17時C.18時D.19時
科目：高中數學 來源： 題型：
【題目】設
，
是兩個平面，
，
是兩條直線，下列命題錯誤的是（ ）
A.如果
，
，那么
.
B.如果
，
，那么
.
C.如果，，
，那么
.
D.如果內有兩條相交直線與平行，那么.
查看答案和解析>>
科目：高中數學 來源： 題型：
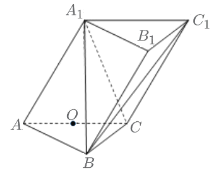
【題目】如圖，在三棱柱
中，側面
底面
，四邊形
為菱形，
是邊長為2的等邊三角形，
，點
為
的中點.
（1）若平面
與平面交于直線
，求證：
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市一所高中為備戰即將舉行的全市羽毛球比賽，學校決定組織甲、乙兩隊進行羽毛球對抗賽實戰訓練．每隊四名運動員，并統計了以往多次比賽成績，按由高到低進行排序分別為第一名、第二名、第三名、第四名.比賽規則為甲、乙兩隊同名次的運動員進行對抗，每場對抗賽都互不影響，當甲、乙兩隊的四名隊員都進行一次對抗賽后稱為一個輪次．按以往多次比賽統計的結果，甲、乙兩隊同名次進行對抗時，甲隊隊員獲勝的概率分別為
，
，
，.
（1）進行一個輪次對抗賽后一共有多少種對抗結果？
（2）計分規則為每次對抗賽獲勝一方所在的隊得1分，失敗一方所在的隊得0分，設進行一個輪次對抗賽后甲隊所得分數為X，求X的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某芯片公司對今年新開發的一批 5G 手機芯片進行測評，該公司隨機調查了 100 顆芯片，所調查的芯片得分均在7，19內，將所得統計數據分為如下：
，
，
，
， 
,
六個小組，得到如圖所示的頻率分布直方圖，其中
.
（1）求這 100 顆芯片評測分數的平均數；
（2）芯片公司另選 100 顆芯片交付給某手機公司進行測試，該手機公司將每顆芯片分別裝在 3 個工程手機中進行初測若 3 個工程手機的評分都達到 13 萬分，則認定該芯片合格；若 3 個工程手機中只要有 2 個評分沒達到 13 萬分，則認定該芯片不合格；若 3 個工程手機中僅 1 個評分沒有達到 13萬分，則將該芯片再分別置于另外 2 個工程手機中進行二測，二測時，2 個工程手機的評分都達到 13萬分，則認定該芯片合格；2個工程手機中只要有 1 個評分沒達到 13 萬分，手機公司將認定該芯片不合格.已知每顆芯片在各次置于工程手機中的得分相互獨立，并且芯片公司對芯片的評分方法及標準與手機公司對芯片的評分方法及標準都一致(以頻率作為概率).每顆芯片置于一個工程手機中的測試費用均為 160 元，每顆芯片若被認定為合格或不合格，將不再進行后續測試．現手機公司測試部門預算的測試經費為 5 萬元，試問預算經費是否足夠測試完這 100 顆芯片?請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
是首項為
，公差為
的等差數列，
是首項為
，公比為q的等比數列．
（1）設
，若
對
均成立，求d的取值范圍；
（2）若
，證明：存在
，使得對n=2，3，···，m+1均成立，并求d的取值范圍（用
表示）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
