
【題目】以下問題最終結果用數字表示
(1)由0、1、2、3、4可以組成多少個無重復數字的五位偶數?
(2)由1、2、3、4、5組成多少個無重復數字且2、3不相鄰的五位數?
(3)由1、2、3、4、5組成多少個無重復數字且數字1,2,3必須按由大到小順序排列的五位數?
【答案】(1)60 (2)72 (3)20
【解析】
(1)五位偶數,要求末位必須是0,2,4,分類求出滿足條件的結果。
(2)可以求出一共能組成多少個五位數,然后再求出2、3相鄰的五位數的個數,兩數相減。
(3)確定數字4,5的排法,然后數字1,2,3按照3,2,1的順序插入。
(1)偶數末位必須為0,2,4對此進行以下分類:
當末位是0時,剩下1,2,3,4進行全排列,![]() =24
=24
當末位是2時,注意0不能排在首位,首位從1,3,4選出有![]() 種方法排在首位,剩下的三個數可以進行全排列有
種方法排在首位,剩下的三個數可以進行全排列有![]() 種排法,所以當末位數字是2時有
種排法,所以當末位數字是2時有![]() =18個數。
=18個數。
同理當末位數字是4時也有18個數,
所以由0、1、2、3、4可以組成無重復數字的五位偶數有24+18+18=60個.
(2)由1、2、3、4、5組成五位數一共有![]() 個。
個。
第一步,把2.3捆定,有![]() 種排法;
種排法;
第二步,捆定的2,3與1,4,5一起全排列,共有![]() 個數,
個數,
根據分步計數原理,2,3相鄰的五位數共有![]()
![]() =48個數,
=48個數,
因此由1、2、3、4、5組成無重復數字且2、3不相鄰的五位數共有
![]() 個數。
個數。
(3)把五位數每個數位看成五個空,數字4,5共有![]() 個,
個,
然后把數字1,2,3按照3,2,1的順序插入,只有一種方式,
根據分步計數原理,可知
由1、2、3、4、5組成無重復數字且數字1,2,3必須按由大到小順序排列的五位數
為![]() 個。
個。


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() .
.
(1)若直線![]() 與直線
與直線![]() 平行,求實數
平行,求實數![]() 的值;
的值;
(2)若![]() ,
, ![]() ,點
,點![]() 在直線
在直線![]() 上,已知
上,已知![]() 的中點在
的中點在![]() 軸上,求點
軸上,求點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)根據兩直線平行,對應方向向量共線,列方程即可求出![]() 的值;(2)根據
的值;(2)根據![]() 時,直線
時,直線![]() 的方程設出點
的方程設出點![]() 的坐標,由此求出
的坐標,由此求出![]() 的中點坐標,再由中點在
的中點坐標,再由中點在![]() 軸上求出點
軸上求出點![]() 的坐標.
的坐標.
試題解析:(1)∵直線![]() 與直線
與直線![]() 平行,
平行,
∴![]() ,
,
∴![]() ,經檢驗知,滿足題意.
,經檢驗知,滿足題意.
(2)由題意可知: ![]() ,
,
設![]() ,則
,則![]() 的中點為
的中點為![]() ,
,
∵![]() 的中點在
的中點在![]() 軸上,∴
軸上,∴![]() ,
,
∴![]() .
.
【題型】解答題
【結束】
16
【題目】在平面直角坐標系xOy中,已知△ABC三個頂點坐標為A(7,8),B(10,4),C(2,-4).
(1)求BC邊上的中線所在直線的方程;
(2)求BC邊上的高所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司制定了一個激勵銷售人員的獎勵方案:當銷售利潤不超過10萬元時,按銷售利潤的15%進行獎勵;當銷售利潤超過10萬元時,前10萬元按銷售利潤的15%進行獎勵,若超出部分為t萬元,則超出部分按![]() 進行獎勵.記獎金為y(單位:萬元),銷售利潤為x(單位:萬元).
進行獎勵.記獎金為y(單位:萬元),銷售利潤為x(單位:萬元).
(1)寫出獎金y關于銷售利潤x的關系式;
(2)如果業務員小王獲得3.5萬元的獎金,那么他的銷售利潤是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,平面
為菱形,平面![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 在棱
在棱![]() 上.
上.
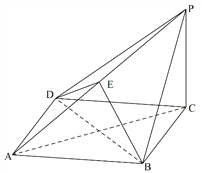
(Ⅰ)求證:直線![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求證:
,求證: ![]() ;
;
(Ⅲ)是否存在點![]() ,使得四面體
,使得四面體![]() 的體積等于四面體
的體積等于四面體![]() 的
的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C1:(x+1)2+(y-3)2=9和圓C2:x2+y2-4x+2y-11=0.
(1)求兩圓公共弦所在直線的方程;
(2)求直線過點C(3,-5),且與公共弦垂直的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數集![]() 具有性質
具有性質![]() :對任意的
:對任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分別判斷數集![]() 與
與![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(Ⅱ)求證![]() ;
;
(Ⅲ)若![]() ,求數集
,求數集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com