
【題目】已知![]() ,其中
,其中![]() .
.
(1)若![]() 是函數
是函數![]() 的極值點,求
的極值點,求![]() 的值;
的值;
(2)求![]() 的單調區間;
的單調區間;
(3)若![]() 在
在![]() 上的最大值是0,求
上的最大值是0,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,增區間是
時,增區間是![]() ,減區間是
,減區間是![]() ;當
;當![]() 時,減區間是
時,減區間是![]() ;當
;當![]() 時,增區間是
時,增區間是![]() ,遞減區間是
,遞減區間是![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)首先求得導函數![]() ,然后根據
,然后根據![]() 求得
求得![]() 的值;(2)首先求得
的值;(2)首先求得![]() 的零點值,然后分
的零點值,然后分![]() 、
、![]() 、
、![]() 討論函數
討論函數![]() 的單調區間;(3)首先由(2)求得函數
的單調區間;(3)首先由(2)求得函數![]() 的最大值,由此求得
的最大值,由此求得![]() 的取值范圍.
的取值范圍.
試題解析:(1)由題意得![]() ,
,
由![]() ,經檢驗符合題意.........................2分
,經檢驗符合題意.........................2分
(2)令![]() ,
,
① 當![]() 時,
時,![]() 與
與![]() 的變化情況如下表:
的變化情況如下表:
|
| 0 |
|
|
|
|
| 0 |
| 0 |
|
| 減 |
| 增 |
| 減 |
∴![]() 的單調遞增區間是
的單調遞增區間是![]() ,
,
![]() 的單調遞減區間是
的單調遞減區間是![]() ........................5分
........................5分
②當![]() 時,
時,![]() 的單調遞減區間是
的單調遞減區間是![]() ,
,
③當![]() 時,
時,![]() ,
,
![]() 與
與![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
| 0 |
|
|
| 0 |
| 0 |
|
| 減 |
| 增 |
| 減 |
![]() 的單調遞增區間是
的單調遞增區間是![]() ,
,
![]() 的單調遞減區間是
的單調遞減區間是![]() ,............................... 8分
,............................... 8分
綜上,當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() ,
,![]() 的單調遞減區間是
的單調遞減區間是![]() ;
;
當![]() 時,
時,![]() 的單調遞減區間是
的單調遞減區間是![]() ;
;
當![]() ,
,![]() 的單調遞增區間是
的單調遞增區間是![]() ,
,![]() 的單調遞減區間是
的單調遞減區間是![]() ,......9分
,......9分
(3)由(2)可知當![]() 時,
時,![]() 在
在![]() 的最大值是
的最大值是![]() ,
,
但![]() ,所以
,所以![]() 不合題意,
不合題意,
當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() 可得
可得![]() 在
在![]() 上的最大值為
上的最大值為![]() ,符合題意,
,符合題意,
∴![]() 在
在![]() 上的最大值為0時,
上的最大值為0時,![]() 的取值范圍是
的取值范圍是![]() ............................12分
............................12分


科目:高中數學 來源: 題型:
【題目】某廠生產![]() 產品的年固定成本為250萬元,每生產
產品的年固定成本為250萬元,每生產![]() 千件需另投入成本
千件需另投入成本![]() 萬元,當年產量不足80千件時
萬元,當年產量不足80千件時![]() (萬元);當年產量不小于80千件時
(萬元);當年產量不小于80千件時![]() (萬元),每千件產品的售價為50萬元,該廠生產的產品能全部售完.
(萬元),每千件產品的售價為50萬元,該廠生產的產品能全部售完.
(1)寫出年利潤![]() 萬元關于
萬元關于![]() (千件)的函數關系;
(千件)的函數關系;
(2)當年產量為多少千件時該廠當年的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠近期要生產一批化工試劑,經市場調查得知,生產這批試劑廠家的生產成本有以下三個部分:①生產1單位試劑需要原料費50元;②支付所有職工的工資總額由7500元的基本工資和每生產1單位試劑補貼所有職工20元組成;③后續保養的平均費用是每單位![]() 元(試劑的總產量為
元(試劑的總產量為![]() 單位,
單位,![]() ).
).
(1)把生產每單位試劑的成本表示為![]() 的函數關系
的函數關系![]() ,并求
,并求![]() 的最小值;
的最小值;
(2)如果產品全部賣出,據測算銷售額![]() (元)關于產量
(元)關于產量![]() (單位)的函數關系為
(單位)的函數關系為![]() ,試問:當產量為多少時生產這批試劑的利潤最高?
,試問:當產量為多少時生產這批試劑的利潤最高?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,點
,點![]() 為坐標原點,若橢圓
為坐標原點,若橢圓![]() 與曲線
與曲線![]() 的交點分別為
的交點分別為![]() (
(![]() 下
下![]() 上),且
上),且![]() 兩點滿足
兩點滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 上異于其頂點的任一點
上異于其頂點的任一點![]() ,作
,作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,且直線
,且直線![]() 在
在![]() 軸、
軸、![]() 軸上的截距分別為
軸上的截距分別為![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
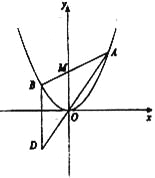
【題目】如圖所示,已知拋物線![]() ,過點
,過點![]() 任作一直線與
任作一直線與![]() 相交于
相交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸的平行線與直線
軸的平行線與直線![]() 相交于點
相交于點![]() 為坐標原點).
為坐標原點).
(1)證明: 動點![]() 在定直線上;
在定直線上;
(2)作![]() 的任意一條切線
的任意一條切線![]() (不含
(不含![]() 軸), 與直線
軸), 與直線![]() 相交于點
相交于點![]() 與(1)中的定直線相交于點
與(1)中的定直線相交于點![]() .
.
證明: ![]() 為定值, 并求此定值.
為定值, 并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 及點
及點![]() ,
,![]() .
.
(1)若直線![]() 平行于
平行于![]() ,與圓
,與圓![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)在圓![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求點
?若存在,求點![]() 的個數;若不存在,說明理由.
的個數;若不存在,說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com