拋擲兩顆骰子,(1)求點數之和為7的概率;(2)求點數之和不小于10的概率.
【答案】
分析:(1)由題意知本題是一個古典概型,試驗發生包含的事件是拋擲兩顆骰子,共有6×6種結果,滿足條件的事件是點數之和是7,可以列舉出所有的事件,共有6種結果,得到概率.
(2)本題是一個古典概型,試驗發生包含的事件是拋擲兩顆骰子,共有6×6種結果,滿足條件點數之和不小于10共有1+2+3=6種結果,根據古典概型概率公式得到結果.
解答:解:(1)由題意知本題是一個古典概型,
試驗發生包含的事件是拋擲兩顆骰子,共有6×6=36種結果,
滿足條件的事件是點數之和是7,可以列舉出所有的事件
(1,6)(2,5)(3,4)(4,3)(5,2)(6,1),共有6種結果,
根據古典概型概率公式得到P=
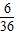
=

(2)由題意知本題是一個古典概型,
試驗發生包含的事件是拋擲兩顆骰子,共有6×6=36種結果,
滿足條件點數之和不小于10,可以列舉出所有的事件
(4,6),(5,5),(5,6),(6,4),(6,5),(6,6),共有6種結果
根據古典概型概率公式得到P=
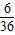
=
 點評:
點評:本題考查古典概型,是一個典型的古典概型問題,本題可以列舉出試驗發生包含的事件和滿足條件的事件,應用列舉法來解題是大綱對這一部分的要求.

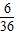 =
=
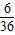 =
=


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案