【題目】設橢圓
的左右焦點分別為
，
，在橢圓L上的點
滿足
，且
，
，
成等差數列．
（1）求橢圓L的方程；
（2）過點A作兩條傾斜角互補的直線
，
，它們與橢圓L的另一個交點分別為B，C，試問直線BC的斜率是否是定值？若是，求出該斜率；若不是，請說明理由．
【答案】（1）
；（2）斜率為
，是定值．
【解析】
（1）由已知
，
，
成等差數列，
，由
結合焦半徑公式可得
，進一步求得
，
結合隱含條件求得b，則橢圓方程可求；
（2）由（1）求得A點坐標，設直線AB的方程為：
，與橢圓方程聯立求得B的坐標，同理求得C的坐標，再由斜率公式可得直線BC的斜率為，是定值．
（1）由，，成等差數列，得
，即，
又，
，即，
聯立①②，解得，
，
．
橢圓L的方程為
；
（2）取
，得
，
，
直線
，
的傾斜角互補，直線，的斜率互為相反數．
可設直線AB的方程為：，代入橢圓方程，得
，
設
，
，點
在橢圓上，
，
，
，
又直線AC的斜率與AB的斜率互為相反數，在上式中以
代替k，可得
，
，
直線BC的斜率
．
故直線BC的斜率為，是定值．
王后雄學案教材完全解讀系列答案
海淀課時新作業金榜卷系列答案科目：高中數學 來源： 題型：
【題目】某職業學校有2000名學生，校服務部為了解學生在校的月消費情況，隨機調查了100名學生，并將統計結果繪成直方圖如圖所示.
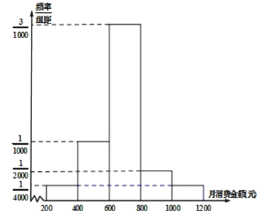
（1）試估計該校學生在校月消費的平均數；
（2）根據校服務部以往的經驗，每個學生在校的月消費金額
（元）和服務部可獲得利潤
（元），滿足關系式：
根據以上抽樣調查數據，將頻率視為概率，回答下列問題：
（i）將校服務部從一個學生的月消費中，可獲得的利潤記為
，求的分布列及數學期望.
（ii）若校服務部計劃每月預留月利潤的
，用于資助在校月消費低于400元的學生，估計受資助的學生每人每月可獲得多少元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動圓M經過點F（1，0），且與直線l：x＝﹣1相切，動圓圓心M的軌跡記為曲線C
（1）求曲線C的軌跡方程
（2）若點P在y軸左側（不含y軸）一點，曲線C上存在不同的兩點A、B，滿足PA，PB的中點都在曲線C上，設AB中點為E，證明：PE垂直于y軸．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的離心率為2，左右焦點分別為
，
，過右焦點且垂直于x軸的直線與雙曲線交于A，B兩點，且
的周長為
．
（1）求雙曲線C的方程；
（2）已知直線
，點P是雙曲線C上的動點，求點P到直線l的距離的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，點
分別是圓心在原點，半徑為
和
的圓上的動點.動點
從初始位置
開始，按逆時針方向以角速度
作圓周運動，同時點
從初始位置
開始，按順時針方向以角速度作圓周運動.記
時刻，點的縱坐標分別為
.
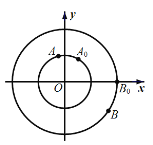
（Ⅰ）求
時刻，兩點間的距離；
（Ⅱ）求
關于時間
的函數關系式，并求當
時，這個函數的值域.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2018·湖南師大附中摸底)已知直線l經過點P(－4，－3)，且被圓(x＋1)2＋(y＋2)2＝25截得的弦長為8，則直線l的方程是________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓E：
，直線l不過原點O且不平行于坐標軸，l與E有兩個交點A，B，線段AB的中點為M．
若
，點K在橢圓E上，
、
分別為橢圓的兩個焦點，求
的范圍；
證明：直線OM的斜率與l的斜率的乘積為定值；
若l過點
，射線OM與橢圓E交于點P，四邊形OAPB能否為平行四邊形？若能，求此時直線l斜率；若不能，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
