
(選修4—1幾何證明選講)已知:直線AB過圓心O,交⊙O于AB,直線AF交⊙O于F(不與B重合),直線l與⊙O相切于C,交AB于E,且與AF垂直,垂足為G,連結AC
 求證:(1)
求證:(1)![]() (2)AC2=AE·AF
(2)AC2=AE·AF
23(選修4—4坐標系與參數方程選講)以直角坐標系的原點O為極點,![]() 軸的正半軸為極軸,且兩個坐標系取相等的單位長度.已知直線
軸的正半軸為極軸,且兩個坐標系取相等的單位長度.已知直線![]() 經過點P(1,1),傾斜角
經過點P(1,1),傾斜角![]() .
.
(I)寫出直線![]() 參數方程;
參數方程;
(II)設![]() 與圓
與圓![]() 相交于兩點A、B,求點P到A、B兩點的距離之積.
相交于兩點A、B,求點P到A、B兩點的距離之積.
24.選修4-5:不等式選講
設函數![]() .
.
(Ⅰ)求不等式![]() 的解集;
的解集;
(Ⅱ)![]() ,使
,使![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
證明:(1)連結BC,由AB為⊙O的直徑所以![]() …………1分
…………1分
又因為![]() …………2分
…………2分
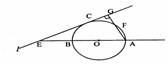 又因為GC與⊙O相切于C,、所以
又因為GC與⊙O相切于C,、所以![]() …………4分
…………4分
所以![]() …………6分
…………6分
(2)由(1)可知![]() ,連結CF
,連結CF
又因為GE與⊙O相切于C,所以![]() 所以
所以![]()
所以![]() …………8分
…………8分
所以![]() 所以
所以![]() …………10分
…………10分
23.解:(I)直線的參數方程是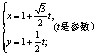 .……………………… 3分
.……………………… 3分
(II)因為點A,B都在直線L上,所以可設它們對應的參數為![]() 則點A,B的坐標分別為
則點A,B的坐標分別為![]()
![]() . …………………………… 5分
. …………………………… 5分
圓![]() 化為直角坐標系的方程
化為直角坐標系的方程![]() .…………………………… 7分
.…………………………… 7分
以直線l的參數方程代入圓的方程![]() 整理得到
整理得到![]() ①
①
因為![]() 是方程①的解,從而
是方程①的解,從而![]() =-2.---------------9分
=-2.---------------9分
所以|PA|·|PB|=![]() =|-2|=2. …………………………… 10分
=|-2|=2. …………………………… 10分
24.解:(Ⅰ)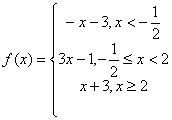 ,------------------------------------------------2分
,------------------------------------------------2分
當![]()
當![]()
當![]()
綜上所述 ![]() ------------------------------------------------------------5分
------------------------------------------------------------5分
(Ⅱ)易得![]() ,若
,若![]() ,
,![]() 恒成立,
恒成立,
則只需![]() ,
,
綜上所述![]() -------------------------------------------------------------------------10分
-------------------------------------------------------------------------10分


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
 A.(選修4-4坐標系與參數方程)已知點A是曲線ρ=2sinθ上任意一點,則點A到直線ρsin(θ+
A.(選修4-4坐標系與參數方程)已知點A是曲線ρ=2sinθ上任意一點,則點A到直線ρsin(θ+| π | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
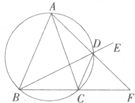 已知△ABC中AB=AC,D為△ABC外接圓劣弧,
已知△ABC中AB=AC,D為△ABC外接圓劣弧, | AC |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•遼寧)(選修4-1幾何證明選講)
(2013•遼寧)(選修4-1幾何證明選講)查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| x+2y |
| xy |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•南京模擬)A.選修4-1幾何證明選講
(2011•南京模擬)A.選修4-1幾何證明選講
|
|
| π |
| 3 |
| 1 |
| abc |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com